ARCHIVE
Vol. 6, No. 1
JANUARY-JUNE, 2016
Research Articles
Research Notes and Statistics
Symposium
Obituaries
Book Review
A Note on the Reliability of Agricultural Wage Data in India:
Reconciliation of Monthly AWI Data
for District-Level Analysis
Takashi Kurosaki* and Yoshifumi Usami†
*Professor, Institute of Economic Research, Hitotsubashi University, kurosaki@ier.hit-u.ac.jp
†Research Fellow, University of Tokyo, yoshiusami@gmail.com
Abstract: We present an overview of the limitations of the agricultural wage data published as Agricultural Wages in India (AWI). We discuss the underlying reasons for these limitations and attempt to address the problems. Through controlling for fixed effects associated with reporting centres and farm operations, we show that it is possible to utilise the AWI data as a source of district-level monthly wage variation without discarding districts with frequent missing data. As changes in reporting centres have a large impact on inter-year dynamics of reported district-level wages, we recommend retaining the same reporting centres over several years in order to improve the quality of the AWI.
Keywords: agricultural wage, missing data, district-level analysis, database of the Indian economy.
1. Introduction
Agricultural Wages in India (hereinafter abbreviated as AWI) are agricultural wage data by district and type of farm operation collected by the Ministry of Agriculture of the Government of India. AWI data have been published in the monthly journal, Agricultural Situation in India, and in the annual publication, Agricultural Wages in India, since 1951–52. AWI is probably the only published source available to researchers that provides continuous and comprehensive data on agricultural wages in the country.1
Although AWI is an important source of wage data in rural India for studying long-term trends of agricultural wages and rural poverty, AWI data have serious limitations, as noted by several authors (e.g., Rao 1972, Jose 1988, Ghanekar 1997, Himanshu 2005, Chavan and Bedamatta 2006). One of these limitations is missing data, which occurs for some reporting centres, months, and farm operations. Unfortunately, there is no established standard in the literature on how to deal with missing data. Among others, Jose (1988) and Chavan and Bedamatta (2006) analysed the long-term trend of agricultural wages in India by constructing time-series data from AWI, focusing on the wage rates for ploughing (males) and weeding (female) at both State and district levels. Since the wage rate for ploughing is comparatively higher than other farm operations in many parts of India, the level of male agricultural wage rate series constructed by these scholars, which does not adjust for this fact, tends to be high and it is likely that they exaggerate male-female and regional disparities. More recently, Berg et al. (2014) analysed the effect of the Mahatma Gandhi National Rural Employment Guarantee Scheme (MGNREGS) on agricultural wages through investigating district-level monthly series based on AWI data. In preparing the district-level monthly dataset, they first aggregated across farm operations without paying attention to the specific operation whose wage was reported, similarly failing to adjust (as they should have done) for differences in the prevalence of specific operations. They then discarded districts where reporting centres were changed over years.
As shown in the study by Berg et al. (2014), AWI is potentially the best source for providing data required for quantitative analysis of the determinants of district-level monthly wage variations, covering a long period and all regions of India. In spite of this potential, there may be a growing hesitation about using AWI, as the problem of missing data, which was already seen from earlier years, has increased recently. Does the problem of missing data of AWI occur randomly, such that unbiased estimates are produced? Given the limitations of AWI data, it is necessary to examine if it is possible to construct an unbroken monthly series of wage rates at the district level for the purpose of analysis over time or across regions. If we can derive reasonably reliable monthly time series at the district level, it would be straightforward to aggregate them to obtain State- and national-level time series. For this reason, we focus in this note on a research question: How should we utilise the AWI data as a source of district-level monthly wage variation? In other words, we do not investigate the extent and reasons for discrepancies across different sources of agricultural wages in India (readers may refer to studies mentioned in the previous paragraph for such attempts).
The objectives of this note are thus to present an overview of the causes of limitations of AWI data (Section 2) and to attempt to mitigate the problems (Sections 3–4). A distinguishing feature of our approach is that we refrain from discarding observations. Given the missing data pattern across reporting centres, farm operations, years, and months, an obvious solution is to discard those with missing data and focus only on districts in which the same centres report wages in almost all months/years and for the same farm operation. This approach is statistically inefficient, however, as it discards useful information included in non-utilised observations. Another solution could be to average over all observations reported for a district for a given month, without paying attention to the (potentially non-random) missing patterns over centres, farm operations, and periods. This approach has the advantage of making the largest number of district-month observations available for analysis but it is likely to suffer from bias as the data missing patterns are not random. Therefore, we attempt to find a way between these two extreme approaches, through employing econometric controls for centres, farm operations, and periods. By retaining all observations, our approach has the advantage of statistical efficiency and by controlling for fixed effects, our approach has the advantage of avoiding bias from averaging “apples and oranges.” Our empirical strategy is explained in Section 3, followed by Section 4, which is on empirical results. Section 5 presents our conclusions, including recommendations for the construction and use of the AWI.
2. Limitations of AWI
2.1. Concept and Definition of Agricultural Wages
The publications and websites connected to the AWI administration provide limited guidance as to the concepts and definitions used in calculating the AWI. According to the proforma provided in the publication (see DES, issues from 1995–96 to 2004–05), it is supposed to collect the “most commonly current” wages in a month in the selected centre (village).2 No definition is given on this awkward expression of “most commonly current.” According to older issues of the publication (Appendix II in DES, issues from 1989–90 to 1994–95), “the wages reported therein should be those most commonly current during the month.” Again, no further explanation was provided. Both the wages in cash and the money value of the wages paid in kind are to be reported. When taking complicated agricultural labour arrangements into consideration, the explanation is completely inadequate. The modes of labour employment and types of wage payments are so complicated and heterogeneous that the mean, median, or another summary statistic concerning all wage employment in a village is unlikely to present an adequate portrait of wage rates. Without more concrete guidance, the “most commonly current” wages can be anything.
Typically, there are both daily labourers and long-term or attached labourers working at different tasks. Some are employed individually by a farmer and some others work together in a group on a contract basis. Some agricultural labourers might be indebted and receive a part of wages in the form of loans, which may or may not be concessional. As for wage payments, there are daily rates and piece rates, and the latter consists of product-based (a fifth of product harvested, for example) or area-based (Rs 1000 per acre, for example) payments. In such cases, we need a conversion factor defining standard work norms per day in order to convert a piece rate to daily wage rate. Working hours per day also vary across farm operations. It is unclear whether a normalisation to eight hours per day or some other standard is undertaken.
When various crops are grown, a variety of farm operations, which vary seasonally, exist. The intensity of farm operations differs according to the crops grown and the conditions of cultivation, between the ploughing of dry and wet land, for example. Furthermore, wage rates for ploughing would vary depending on who owns a plough and a pair of bullocks. Over the last four to five decades, farm operations have changed significantly in the direction of mechanisation. Ploughing with bullocks has been replaced by tractor ploughing. It is not certain if AWI collects a separate wage rate for tractor ploughing. Regardless, if wages for ploughing are paid by piece rates based on area, it would be very difficult to calculate the wage rate per day for human labour after deducting animal or machine rent.
These are only a few examples of the complicated nature of agricultural labour arrangements that suggest how difficult it is to collect the “most commonly current” wage rate in a village. It may be difficult to identify a wage rate that is characteristic of various farm operations in a village.
It is plausible, however, that standard wage rates and norms exist for each specific farm operation performed by males, females, and children. These are supposedly what AWI tries to capture, as the agency is described as collecting this standard wage rate for each farm operation based on information provided by villagers and their understanding of the locally relevant current wage rate. However, the wage rate collected by the AWI reporting agency is the expenditure on labour rather than the wage rate received by agricultural workers. The wage data thus collected do not necessarily represent any particular class or category (Himanshu 2005).
2.2. Selection of Districts and Centres (Villages)
Unlike the methodology adopted in “Wage Rates in Rural India” compiled by the Labour Bureau, it is unclear how primary data are collected in the AWI administration. According to the “Explanatory Notes,” State governments are supposed to report the information on agricultural wages for each district. The selection of districts is left to the State government and many States do not report wage data in all districts. In some States, the number of reporting districts is small, only ten districts in Uttar Pradesh from 1973–74 to 1994–95, for example. Thus the wage rates reported in AWI do not necessarily represent the employment situation in the whole of a State. Besides, all the selected districts do not always report regularly and, as a result, the number of reporting districts varies frequently. Moreover, the number of reporting districts has recently decreased, from 15 in 2005–06 to 9 in 2009–10 in Bihar, for instance. The State of Maharashtra did not report wages at all in 2004–05 and 2009–10, and the State of West Bengal did not report wages in 2008–09 and 2009–10.
There is no instruction manual for the selection of centre(s) in a district and the task is left to district headquarters. It is thus doubtful if villages are selected representatively in the district, taking agro-climatic conditions and the employment situation into account. Given the substantial variation in wages across villages within a district, it is unlikely that the sample centres selected represent labour market situations in the district or in the State. In his reliability study, Rao (1972) noted that the choice of bigger villages near a town as reporting centres is a cause of upward bias of AWI wages compared to other wage data sources, such as the National Sample Surveys and Farm Management Studies. As changes in reporting centres often take place and because it is not clear whether a village is replaced by another village with a similar employment situation, irregular fluctuation might occur when a centre is replaced by another village that has different employment characteristics.
2.3. Reporting Agency
A primary reporting agency in a selected centre has to send the returns to the district headquarters, which are responsible not only for the accuracy of the data furnished but also for their timely submission to their State headquarters. No information, however, is given as to who are the primary reporting agencies. It is likely that a village accountant (patwari, for example) is the primary reporting agency in most districts where the institution of patwari exists. In such a case, since he is a village-level official of the revenue administration, it is not certain whether he sends the returns on agricultural wages every month to the office of the agricultural department. Instead, he may postpone sending the wage returns until his regular reports, such as area under crops, are sent to the revenue department. The collection of agricultural wage data is considered to be a minor duty among other, more important ones. Hence an attitude of indifference creeps in among field investigators as well as other agencies involved in the reporting process (Ghanekar 1997).
A cursory look at AWI data shows that agricultural wages are not reported regularly, and patterns of non-reporting are difficult to explain in terms of seasonality of farm operations. For example, wages for ploughing or harvesting are reported every month, which may be unrealistic in some areas. To take another example, wages for all four farm operations (ploughing, sowing, weeding and harvesting) are reported in a single month and no wages at all are reported in other months, which also appears unrealistic. The first case creates the suspicion that the reporting agency sends returns every month without confirming the actual farm operations performed. The second case creates the suspicion that the reporting agency does not care to send the returns on wages for each farm operation every month. It is, however, difficult to discern whether irregular reporting is caused by the seasonality of farm operations or by the negligence of reporting agencies.
2.4. Missing Data and Replacement of Reporting Centres
Along with the problems mentioned above, serious problems with AWI are missing data and the replacements of sample centres by new centres. There are two types of missing data, districts (or centres) for which data are missing and missing data on specific farm operations. There are numerous districts for which no wage data was reported for several years. Centre-district combinations are summarised in Appendix Table 1 during the five agricultural years (2005–06 to 2009–10) as an example.3 In Bihar, only 5 districts out of the selected 25 districts reported at least one month every year; at the same time, data for one to four years were missing in the remaining districts. In Rajasthan, out of 32 districts selected, only 8 districts reported every year, and data for one to four years was missing for each of 24 districts.
In addition, there were frequent changes in reporting centres. In Tamil Nadu during the same five years, out of 29 selected districts, the number of districts with no change in the list of reporting centres with full information over all five years was zero. The number of districts with no change in the centres but for which information was missing in the first and second years was 14 out of 29; in the remaining 15 districts, centres were replaced once or two times. In Bihar, continuous data were available for at least one centre in each of four districts; in all other districts, either the problem of replacement of centres or of non-reporting occurred.
Non-reporting and replacement pose serious problems. Given a large variation in employment situation and wage rates across districts, the missing data at the district level may cause an irregular fluctuation when State-wise time-series data are constructed with an insufficient number of sample districts. This is why Chavan and Bedamatta (2008) used district data rather than constructing State-wise wage data. Their method, however, raised another question of whether the districts selected based on data availability represent the agricultural labour market conditions of the State.
Missing data becomes a more frequent problem when we look at the operation-wise monthly wage data. Other than for some States like Andhra Pradesh and Karnataka where wage rates for aggregated category (“field labour”) are reported, wage rates for four operations (ploughing, sowing, weeding and harvesting) or more are reported. Nevertheless, it is rare that monthly wage rates for all farm operations are reported. As mentioned above, farm operations are characterized by seasonality. When the farm operation is not performed, no wage rate is supposed to be reported. In AWI data, however, we sometimes observe wages for farm operations which appear unlikely to have been conducted in a particular month. For example, ploughing generally starts just before monsoon for kharif crops and then again before rabi crop sowing. Though there may be fallow ploughing, it is unrealistic that ploughing is performed throughout a year. In other problem cases, wages for ploughing are reported for some months in one year but not reported in the next year.
Since the wage rate for ploughing is higher than wages for other farm operations, missing data on wages for ploughing may cause irregular fluctuations in district-level monthly wage data, if we calculate the average over all operations whose data are available. An example is Kottayam District in Kerala, where the average of available wage data shows a sudden upsurge in 2008–09 and a drop in 2009–10, the change being caused by the presence or absence of data on wages for ploughing.
3. Data and Empirical Strategy
3.1. Choosing the State and Period Coverage
Among the several problems summarised above, we focus on the problem of missing data in the rest of this note. Given the raw data reported in DES (various issues), which have frequent missing data problems, how can we utilise the AWI data as a source of district-level monthly wage variation? This is the main research question addressed below.
As the purpose of this note is to present an exploratory methodology, we examine the research question with respect to male wages in selected States of India for selected years only. Specifically, we analyse a period of five agricultural years, 2005–06 to 2009–10.
We selected States with diverse patterns of missing data, resulting in the choice of Tamil Nadu, Rajasthan, Bihar, and Andhra Pradesh. Tamil Nadu is a case with less frequent missing data, and farm operations well spread over a year, but with only one reporting centre for one district. Each centre reports wages for one to several years. Rajasthan had a moderate number of missing observations. Except for one district, for which two centres reported exceptionally in one year, there was only one reporting centre for one district in Rajasthan. In this aspect, the case of Rajasthan is similar to the case of Tamil Nadu. In these cases, how to link different years with data from different reporting centres was a critical question. Bihar is a case where several districts had multiple reporting centres in the same year, so that the aggregation across centres was an important issue. Unfortunately, however, Bihar had a large number of missing observations. Finally, Andhra Pradesh is a case where only one aggregated category (“field labour”) was reported, without details on farm operation-wise differences.
3.2. Data
Let us introduce some notations, as they will facilitate the theoretical discussion later in this section. We are interested in analyzing the natural log of real wage for males in district d of one of the four States in period t, which is denoted by wagedt. We use a capitalised word to denote levels before the log-transformation (i.e., wagedt = ln(Wagedt)). The period t is measured in monthly intervals (i.e., the combination of the agricultural year and month of the year determines t). As we cover five agricultural years from 2005–06 to 2009–10, there are 60 periods.
From the AWI data, we obtain monthly wage levels further distinguished by the reporting centre (subscript c) and farm operation (subscript k). One district has one or more reporting centres in AWI. We divided the AWI raw data by the CPI-AL (consumer price indices for agricultural labourers) published in various issues of Labour Bureau, Government of India, to convert them into real 2005–06 prices for each State. Let wagecdkt stand for the natural log of the real wage in centre c in district d for operation k in period t (as before, wagecdkt = ln(Wagecdkt)).
Table 1 shows summary statistics of Wagecdkt and wagecdkt. As expected, real wages were higher in Tamil Nadu and Rajasthan than in the other two States. The real wage level in Bihar was the lowest among the four. Real wages have large standard deviations, potentially reflecting trends, seasonality, heterogeneity because of farm operations, and heterogeneity because of reporting centres.
Table 1 Summary statistics of male agricultural wages, four selected States of India, 2005–06 to 2009–10
| Number of observations | Mean | Std. Dev. | Min | Max | Number of reporting districts | Average number of observations per district | |
| Tamil Nadu | |||||||
| Wage | 2627 | 85.5 | 26.9 | 27.9 | 238.2 | 29 | 90.6 |
| wage | 2627 | 4.41 | 0.29 | 3.33 | 5.47 | 29 | 90.6 |
| Rajasthan | |||||||
| Wage | 1452 | 85.3 | 29.3 | 36.3 | 263.1 | 32 | 45.4 |
| wage | 1452 | 4.39 | 0.32 | 3.59 | 5.57 | 32 | 45.4 |
| Bihar | |||||||
| Wage | 1051 | 62.0 | 15.8 | 25.3 | 140.3 | 25 | 42.0 |
| wage | 1051 | 4.10 | 0.24 | 3.23 | 4.94 | 25 | 42.0 |
| Andhra Pradesh | |||||||
| Wage | 1756 | 70.6 | 19.3 | 30.1 | 165.2 | 22 | 79.8 |
| wage | 1756 | 4.22 | 0.27 | 3.40 | 5.11 | 22 | 79.8 |
Notes: "Wage" is a real wage measured in rupees (Rs) per day, where Rs refers to the 2005–06 prices in each State; "wage" is the natural log of "Wage."
Std. Dev.=standard deviation
Source: Compiled by the authors using AWI and CPI-AL data (see the text for details).
Table 1 also reports the average number of observations per district. As the average is above 60 (the number of periods covered in our analysis) in Tamil Nadu and Andhra Pradesh, it appears promising to compile district-level monthly data for all reporting districts in these two States. Because of frequent occurrences of missing data, the average is much below 60 in Rajasthan and Bihar, which could make it difficult to compile such data for those two States. Missing data problems in Bihar are more serious than in Rajasthan because the number of centres per district is much larger in Bihar than in Rajasthan (see Appendix Table 1 for the centre-wise distribution of our data).
As an illustration, we pick up the district of Coimbatore from Tamil Nadu (the first district in alphabetical order) and plot all observations from this district in Figure 1.
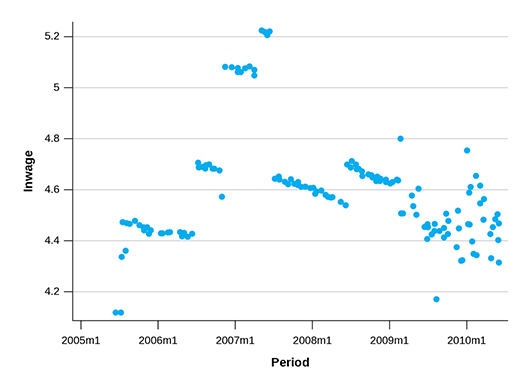
Figure 1 Distribution of Wage Observations in Coimbatore, Tamil Nadu
Note: There are 161 observations plotted in this figure. “wage” (natural log of real wage per day) is plotted on the vertical axis. As several observations fall on the same value in a period, the STATA option “jitter” is used to plot them horizontally.
One is tempted to conclude that an inverted-U shape change occurred in this district over the five years and the short-run variation increased in more recent years. However, this plot mixes up wages from different centres and different farm operations. Many of the changes shown in Figure 1 could be spurious, without actual changes in the field. In the case of Coimbatore, three different centres reported wages: Myleripalayam in 2005–06, Vellalore in 2006–07, and Narasipuram from 2007–08 to 2009–10. In the case of Coimbatore, wages from various farm operations were reported simultaneously in the same month.
3.3. Three Naïve Approaches
We would like to obtain district-level monthly data, defined as
wagedt = E{c,k}[wagecdkt] (1)
where E[.] is the expectation operator. As an empirical proxy for this, a naïve approach could be to use the simple average to replace E[.]:
wage′dt = Σ{c,k}[wagecdkt]/Ndt, (2)
where Ndt is the number of observations in wages in period t in district d. Let us call this measure “All_Avg”. Although this approach guarantees the maximum number of district-level monthly observations, it could be very biased, as suggested in Figure 1.
At the other extreme, we can choose one c as the most representative reporting centre and one k as the most representative farm operation. The centre (farm operation) associated with the largest number of observations is the natural choice for representativeness. Let us call this “Same_Ope”, as this approach is based on the same farm operation. Because of frequent missing observations, this approach has the drawback of covering the smallest number of observations available for each district.
As a compromise between the two approaches, the third naïve approach is to take the simple average over farm operations in each centre and then choose the centre that can be regarded as the most representative for the district (again using the largest number of observations as the criteria for representativeness). This approach is essentially the same as the one adopted by Berg et al. (2014). Let us call this “Ope_Avg”, as it averages over operations only, without aggregating over different centres.
We plot the three naïve estimates for Coimbatore in Figure 2. “All_Avg” is just a smoothed series of Figure 1. It has the advantage of covering a large number of observations but appears subject to substantial bias. We suspect that an abrupt increase in wages in the second agricultural year 2006–07 was spurious, as the centre that reported wages in that year was generally associated with higher wages. “Same_Ope” (we adopt the wage of “harvester” as the most representative farm operation and Narasipuram as the most representative centre) has the advantage of relatively better comparability but the number of observations involved is small. In the particular case of Coimbatore, the advantage of “Ope_Avg” over “Same_Ope” is very small in terms of the number of observations. Only one observation is added (2008m5 is missing for “Same_Ope” but available for “Ope_Avg”). In general, when the number of observations per district in a given month is small, the three naïve estimates for a district become highly similar. Figure 2 shows that this is indeed the case for Coimbatore. We obtain similar results for other districts as well.
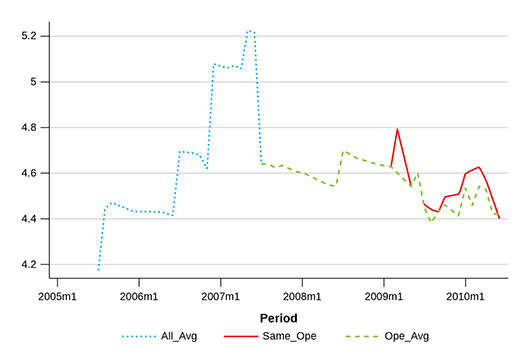
Figure 2 Naïve Estimates of Monthly Wages in Coimbatore, Tamil Nadu
Notes: Estimates for “wage” (natural log of real wage per day) is plotted on the vertical axis. “All_Avg” spans all five years. In the first two years, it is shown in the dotted line. In the last three years, it is shown in the dashed line as it overlaps completely with “Ope_Avg”. “Same_Ope” spans the last three years except for 2008m5, which is missing. It is shown in either the solid line or dashed line. “Ope_Avg” spans the last three years, shown in the dashed line.
In our opinion, discarding all information in the first two years in Figure 1 (as in “Same_Ope” or “Ope_Avg” in Figure 2) is too costly a method. We would prefer to keep all information while minimising the potential bias suggested in “All_Avg” in Figure 2. This is the first principle. Comparing “Same_Ope” and “Ope_Avg” (or “All_Avg” when all three estimates are available), we gain the impression that intertemporal change across months is more reliable in “Same_Ope,” since it is based on the same farm operation, while “Ope_Avg” and “All_Avg” are averages over different operations, whose combination differs from month to month. We would like to extract the maximum information from the intertemporal change that occurred in the same centre for the same farm operation. This is the second principle. Our alternative approach, given below, attempts to satisfy the two principles as much as possible.
3.4. Fixed Effect Approach
When does the approximation (2) give the unbiased estimate for (1)? Suppose a data-generating process that is linearly additive in year, month, centre, district and operation specific effects, augmented by an idiosyncratic shock at the cdkt level:
wagecdkt = yeart + montht + γd + γc + γk + ucdkt (3)
where yeart is an effect specific to the agricultural year (e.g., macroeconomic fluctuations), montht controls for seasonality specific to a month of a year, γd is a district-specific effect (e.g., districts with larger [smaller] nonagricultural labour demand have higher [lower] agricultural wages), γc is a centre-specific effect (e.g., centres close to [far away from] a town with large nonagricultural labour demand have higher [lower] agricultural wages), γk is an operation-specific effect (e.g., some farm operations require hard labour so wages are higher than for other operations) and ucdkt is an idiosyncratic shock. With a normalisation with zero mean for γc and γk, respectively, the district-level monthly wage is derived as
wagedt = yeart + montht + γd + E{c,k}[ucdkt] (4)
Comparing equations (1)–(4) readily reveals that equation (2) is unbiased when (i) wage′dt and γc are orthogonal, and (ii) wage′dt and γk are orthogonal, i.e. the traits of the centres or operations are not systematically linked to whether or not observations are missing. Description of the institutional background in Section 2 suggests, however, that data are missing non-randomly across centres and farm operations. Therefore, we expect conditions (i) and (ii) are not satisfied so that equation (2) is biased. However, the size of the bias depends on: (iii) the size of variation of γc and γk, and (iv) the extent of non-randomness. These are empirical issues to be analysed in the rest of this paper.
As the true data-generation process is never known in real economy data, we infer it from the data from three ways. In other words, our empirical strategy comprises the following three analyses.
First, we test whether data went missing in specific centres and farm operations independently of period t. If the correlation between the missing data pattern and time is sufficiently weak, the approximation (2) might be justified.
Secondly, the size of variation of γc and γk is empirically investigated through estimating equation (3). The equation is estimated by the method of analysis of variance (ANOVA) or fixed effect ordinary least squares (OLS). In the case of fixed effect OLS, γd and γc are perfectly collinear by construction, so that they are not separately identified. We drop γd in the fixed effect OLS estimation.
Thirdly, we compare time series of district-level wages in a graphical way: the naïve approach based on equation (2) called “All_Avg,” and our preferred approach of controlling for centre and operation specific effects. We control for centre- and operation-specific effects in the following three steps. In the first step, we estimate equation (3) using the fixed effect OLS and then normalise the fitted values of γc and γk with zero means. In the second step, we subtract the normalised fitted values of γc and γk from observed data of wagecdkt. In the last step, we take averages of this series over c and k to obtain our estimates for wagedt. Ideally, we need to adopt weighted regressions in estimating equation (3) and use weighted averages to obtain the district-level data. The weights should reflect the differential importance of different farm operations in each centre and the differential importance of different centres in each district. As the information on such weights is not available at the centre or district level, we use unweighted averages. We call the estimates thus obtained “FE_Control” and compare it with “All_Avg.” We do not include “Ope_Avg” in the comparison as it is mostly a part of “All_Avg” and its utility is highly limited because of the small number of observations the approach can facilitate.4
4. Empirical Results
4.1. Independence of Missing Data Patterns
Table 2 summarises the test results for independence of missing data patterns. The whole distribution of our observations underlying the tests is provided in Appendix Table 1 (centres vs. years) and Appendix Table 2 (farm operations vs. years; farm operations vs. months).
Table 2 Independence of “data missing” patterns
| Agricultural years | Months within a year | |||||
| Chi2 | p-value | Chi2 | p-value | |||
| A. Distribution of farm operations | ||||||
| Tamil Nadu | Chi2(16) | 118.00 | 0.000 | Chi2(44) | 55.047 | 0.123 |
| Rajasthan | Chi2(12) | 7.69 | 0.809 | Chi2(33) | 70.646 | 0.000 |
| Bihar | Chi2(12) | 75.26 | 0.000 | Chi2(33) | 14.296 | 0.998 |
| B. Distribution of reporting centres | ||||||
| Tamil Nadu | Chi2(200) | 4.3e+03 | 0.000 | Chi2(550) | 259.15 | 1.000 |
| Rajasthan | Chi2(152) | 977.63 | 0.000 | Chi2(418) | 642.97 | 0.000 |
| Bihar | Chi2(140) | 1.3e+03 | 0.000 | Chi2(385) | 55.047 | 0.000 |
| Andhra Pradesh | Chi2(260) | 1.0e+03 | 0.000 | Chi2(715) | 20.489 | 1.000 |
Notes: The null hypothesis that the distribution of observations across farm operations (or reporting centres) is independent of the distribution of observations across agricultural years (or months within a year) is tested by the chi-square test.
Unexpectedly, the hypothesis of independence between the distribution of farm operations and the distribution of months is not rejected in Tamil Nadu and Bihar. If specific farm operations were reported only in a limited number of months within a year, the null hypothesis of independence is rejected, as happened in Rajasthan. In Tamil Nadu, where agriculture is diverse and irrigation enables continuous farming throughout a year, wages for farm operations were reported in a balanced way throughout a year, resulting in the statistical non-rejection. Bihar appears slightly different. As wages were reported only sporadically in this State, any statistical test tends to fail to reject the null hypothesis because of the lack of statistical power. On the other hand, it is a serious concern that the independence between the distribution of farm operations and the distribution of years is rejected in Tamil Nadu and Bihar. In Tamil Nadu, wages for “weeder” are concentrated in recent years while wages for “ploughmen” are concentrated in the year 2006–07; in Bihar we have few reports for “ploughmen” or “reaper” in years with fewer observations than others (see Appendix Table 2). In other words, data reporting with regard to farm operations changed across years in these two States.
As shown in the second panel of Table 2, the hypothesis of independence between the distribution of centres and the distribution of years is strongly rejected in all four States. This reflects the institutional background in which the change of centres occurs across agricultural years. The same panel shows that the independence between the distribution of centres and the distribution of months is rejected in Rajasthan and Bihar while it is not rejected in Tamil Nadu and Andhra Pradesh. In Tamil Nadu and Andhra Pradesh, there are not many cases where a centre did not report any wage, resulting in non-rejection. In Bihar and Rajasthan, where missing data within a year occurred more frequently, the exact months when data were missing differed from centre to centre, resulting in rejection.
The results in Table 2 thus show that the missing data pattern is not random. This raises the concern for a potential bias in the approximation (2).
4.2. Sources of Wage Variations
The potential bias in approximation (2) is empirically negligible if the size of variation of γc and γk is small. To examine whether this holds, we apply ANOVA to equation (3). The results are summarised in Table 3.
Table 3 Sources of wage variations (ANOVA results)
| Tamil Nadu | Rajasthan | Bihar | Andhra Pradesh | |||||||||
| Partial SS | F-stat | p-value | Partial SS | F-stat | p-value | Partial SS | F-stat | p-value | Partial SS | F-stat | p-value | |
| Model | 110.90 | 39.01 | 0.000 | 82.85 | 30.51 | 0.000 | 31.01 | 20.09 | 0.000 | 77.81 | 35.33 | 0.000 |
| year | 6.34 | 38.45 | 0.000 | 1.86 | 9.58 | 0.000 | 0.46 | 3.93 | 0.004 | 16.98 | 154.20 | 0.000 |
| month | 0.19 | 0.42 | 0.946 | 1.00 | 1.88 | 0.038 | 0.32 | 1.01 | 0.431 | 0.36 | 1.19 | 0.286 |
| district | 53.25 | 46.16 | 0.000 | 50.07 | 33.31 | 0.000 | 15.73 | 22.51 | 0.000 | 15.84 | 27.41 | 0.000 |
| centre | 10.87 | 11.99 | 0.000 | 1.25 | 3.69 | 0.001 | 2.65 | 8.28 | 0.000 | 16.55 | 13.66 | 0.000 |
| operation | 14.31 | 86.81 | 0.000 | 10.48 | 72.04 | 0.000 | 3.41 | 39.02 | 0.000 | |||
| Residual | 105.36 | 67.65 | 29.03 | 46.11 | ||||||||
| Total | 216.26 | 150.50 | 60.03 | 123.92 | ||||||||
| N | 2627 | 1452 | 1051 | 1756 | ||||||||
| R2 | 0.513 | 0.551 | 0.517 | 0.628 | ||||||||
| adj. R2 | 0.500 | 0.532 | 0.491 | 0.610 | ||||||||
Notes: The variance decomposition model is equation (3) in the text. The null hypothesis that the model has no explanatory power is tested by the F test.
Year, district, centre, and farm operation specific effects contribute to the wage variation with the statistical significance level at the 1 per cent level or lower. On the other hand, month specific effects have no explanatory power in Tamil Nadu, Bihar, and Andhra Pradesh. Once we take account of the within-year inflation by CPI-AL, seasonality is not statistically significant, other than for Rajasthan.5
In Figure 3, we plot the estimated coefficients of year-fixed effects, estimated by a fixed effect OLS (or ANCOVA), normalised with zero for the first agricultural year. Andhra Pradesh experienced high and steady growth in wages, followed by Rajasthan. Wage rates in Bihar stagnated over the five-year period.
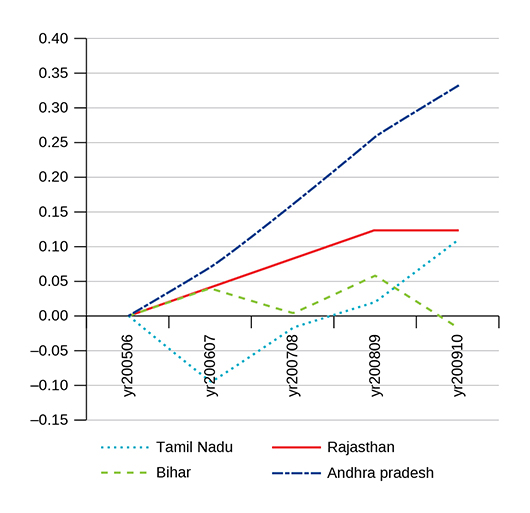
Figure 3 Annual Change in Log of Real Agricultural Wages
Notes: This figure plots the fitted values of year fixed effects in log of real wages, with normalisation of 0 for the first agricultural year. The vertical axis can be interpreted as the multiplicative factor. For instance, 0.10 means that the log wage was 10% higher than the level in year 2005–06 (the wage was 10.52% higher than the level in year 2005–06, where exp(0.1)=1.1052).
Figure 3 shows an initial decline followed by a recovery in Tamil Nadu. Because of a drastic churning of reporting centres in Tamil Nadu between the second and third years (see Appendix Table 1), the year fixed effects plotted in Figure 3 for Tamil Nadu are potentially subject to weak identification. The growth rate between yr2005–06 and yr2006–07 and two growth rates in yr2007–08 and yr2009–10 are well identified from several centres, whereas the growth rate between yr2006–07 and yr2007–08 is identified through only one centre (Vellampatti Centre in Dharmapuri District). If some abnormal change occurred in this centre, the whole shape of year fixed effects in Tamil Nadu is affected. In other words, our methodology does not work well if reporting centres are changed every year, as it becomes difficult to clearly distinguish centre fixed effects from year fixed effects.
In Figure 4, we plot the estimated coefficients of operation-fixed effects. Weeding, which is regarded as light work, is paid much less than ploughing. The harvesting wage relative to ploughing wage was different among the three States: they were at a similar level in Tamil Nadu while the harvesting wage was much lower than the ploughing wage in Rajasthan; Bihar lay in between.
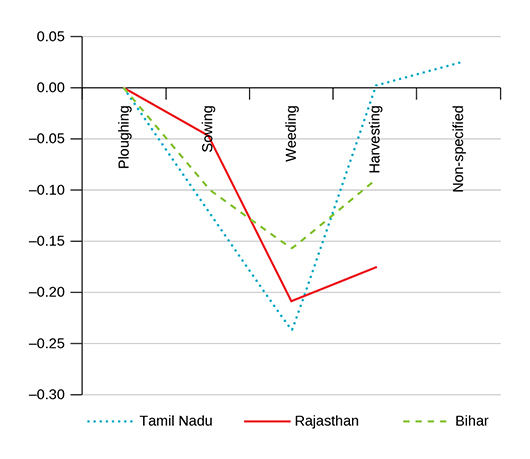
Figure 4 Differential in Log of Real Agricultural Wages according to Farm Operations
Notes: This figure plots the fitted values of farm operation fixed effects in log of real wages, with normalisation of 0 for the ploughing work. The vertical axis can be interpreted as the multiplicative factor. For instance, -0.10 of sowing in Bihar means that the log wage in sowing was 10% lower than the level in ploughing (the sowing wage was 9.52% lower than the ploughing wage, where exp(-0.1)=0.9048).
For our purpose, the considerable centre and operation specific effects raise a serious concern, as we would like to obtain district-level monthly wages. Figure 4 suggests the potential bias of approximation (2) if we ignore the fact that data are missing across farm operations non-randomly with respect to years (Tamil Nadu and Bihar) or months (Rajasthan). It is not a straightforward task to interpret a comparable chart for centre fixed effects, so instead, we report standard deviations of their fitted values: 0.213 (Tamil Nadu), 0.241 (Rajasthan), 0.158 (Bihar), and 0.185 (Andhra Pradesh). Please note that the standard deviations are a natural proxy for the size of variation of γc in equation (3). These magnitudes are indeed large in comparison to averages of log wages reported in Table 1. This suggests the potential bias of approximation (2) if we ignore the fact that data are missing across centres non-randomly with respect to years (all four States) or months (Rajasthan and Bihar).
4.3. Comparison of District-Level Monthly Series
In Appendix Table 1, we put an asterisk to a district for which we can obtain 5-year estimates based on the “All_Ave” and “FE_Control” approaches. The number of such districts is 14 out of 29 for Tamil Nadu, 8 out of 32 for Rajasthan, 5 out of 25 for Bihar, and 17 out of 22 for Andhra Pradesh.6 In this subsection, we selectively show the results of graphical comparison that merit comments.7
We first describe “FE_Control” estimates in detail for the case of Coimbatore District, Tamil Nadu, as this district was discussed in the previous section in the form of Figure 2. Two estimates under “All_Ave” (dotted line) and “FE_Control” (solid line) are plotted in Figure 5A. First, the inverted U-shape of the “All_Ave” series in Figure 2 disappears from the “FE_Control” series in Figure 5A (as comparison purpose, the “All_Ave” series is plotted in Figure 5A as well). The conjecture in the previous section that a centre specific factor spuriously creates the inverted U-shape is confirmed. If we control for centre-fixed effects, there is no inverted U-shape over the five year span. It is almost flat or slightly increasing. Based on other information from the district, we judge that the shape in the “FE_Control” series is more likely to describe the actual change in Coimbatore during the five years than the “All_Ave” series. Second, in the last three agricultural years, where the same centre reported wages, the “FE_Control” and “All_Ave” are almost similar, but with slightly different short-run dynamics. For example, between 2009m2 and 2009m3, “FE_Control” shows an increase in the wage, whereas “All_Ave” shows a decrease. Comparing Figure 2 and Figure 5A, we find that the movement in “FE_Control” is consistent with the actual change that occurred in the wage of harvesters as shown in “Same_Ope” in Figure 2. This indicates the importance of controlling operation fixed effects when we investigate short-run wage movements in a district within a year. In other words, as we control for farm operation-fixed effects, the “FE_Control” series successfully eradicates some of the short-run fluctuations that are spuriously observed due to changes in the mixture of farm operations for which wages were reported.
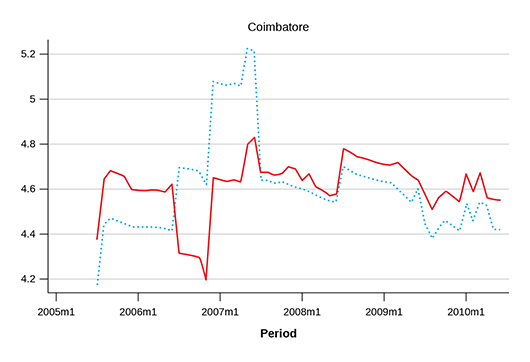
Figure 5A Two Estimates of Monthly Wages in Coimbatore, Tamil Nadu
Notes: Estimates for district-level monthly wage (natural log of real wage per day) is plotted on the vertical axis. The dotted line is reproduced from Figure 2, corresponding to the “All_Avg” estimate. The solid line shows the “FE_Control” estimate. These notes are applicable to all figures below.
In Figure 5B, two estimates are plotted for selective districts out of the remaining 13 districts for which 5-year district-level monthly data can be estimated. As shown in Appendix Table 1, there was no change of reporting centres in Tamil Nadu in the final three years. Therefore, the comparison of solid and dotted lines in the last three years will tell us the impact of controlling farm operation fixed effects. As reporting centres changed in the first three years, the comparison of solid and dotted lines for the first three years will tell us the impact of controlling both centre and operation fixed effects.
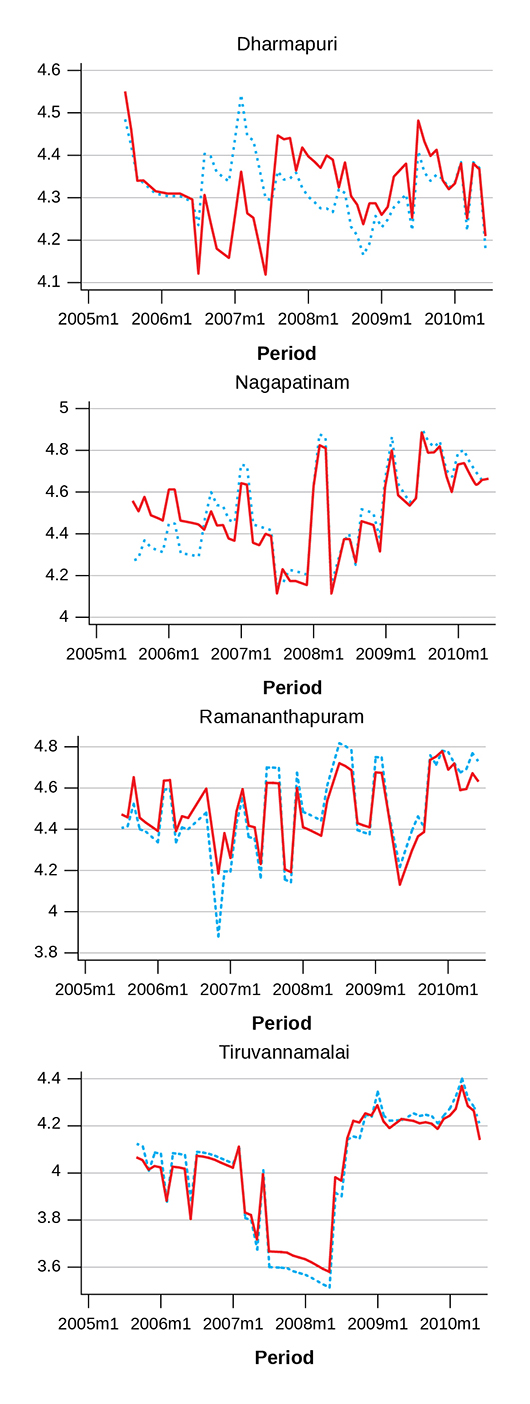
Figure 5B Two Estimates of Monthly Wages in Other Districts, Tamil Nadu
The first finding from the Coimbatore case that centre fixed effects matter substantially is robustly supported by our findings from four other districts in Figure 5B. The difference is striking especially for Dharmapuri and Nagapatinam. Dotted lines (“All_Ave”) and solid lines (“FE_Control”) show completely different inter-year dynamics, and we judge the movement shown in dotted lines is likely to be spurious due to centre specific factors. In the two remaining districts of Ramananthapuram and Tiruvannamalai, the divergence between dotted and solid lines is small but still the inter-year movement shown in solid lines (“FE_Control”) appears to be more stable. The case of Dharmapuri District is important as there was an unusual churning of reporting centres (see Appendix Table 1) that one centre (Vellampatti) revived after discontinuation, enabling the identification of centre and year fixed effects (see Subsection 4.2). The second finding from the Coimbatore case that farm operation fixed effects do not make a big difference but occasionally show the opposite directions of short-run changes between months in a year is again supported from the four other districts in Figure 5B.
Figure 5C shows two estimates for four selected districts in Rajasthan for which 5-year district-level monthly data can be estimated. Ajmer is a case where one centre reported wages in the first two years and then another centre reported wages in the last three years. Baren and Pali are cases where one centre reported wages throughout the five years so the dotted line-solid line difference is solely due to operation fixed effects. Baren has a reasonable number of observations (14.8 per year on average) while Pali suffers from more frequent missing data (7.2 observations per year on average). In Tonk, one centre reported wages throughout the five years and another centre reported wages in the second year only. This is a case where the aggregation problem of different centres arises.
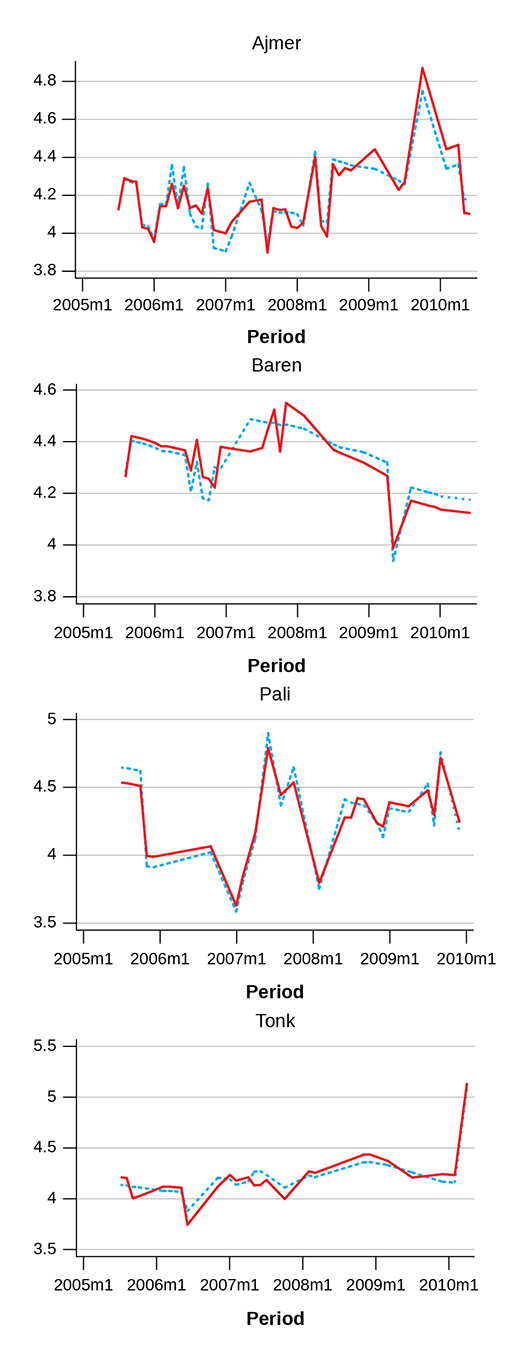
Figure 5C Two Estimates of Monthly Wages in Selected Districts of Rajasthan
Unlike the case of Tamil Nadu, inter-year connection is smooth for both Ajmer and Tonk regardless of the choice of “All_Ave” and “FE_Contrl”. It appears that centres were chosen to represent the district well in these two districts. Whether this interpretation can be applied to all districts in Rajasthan remains an open question since data in Rajasthan suffer from too frequent problems of missing data. Similar to the case of Tamil Nadu, farm operation fixed effects do not make a big difference but occasionally show the opposite directions of short-run changes between months in a year, especially in Baren District.
Figure 5D shows two estimates for four selected districts in Bihar. Darbhanga and West Champaran are cases where there were two centres that reported wages, one of which did so continuously and the other did so with missing years. In Madhubani, three centres were churning during the three years. Vaishali is a case where one centre reported wages throughout the five-year period, so the dotted line-solid line difference is solely due to operation fixed effects.
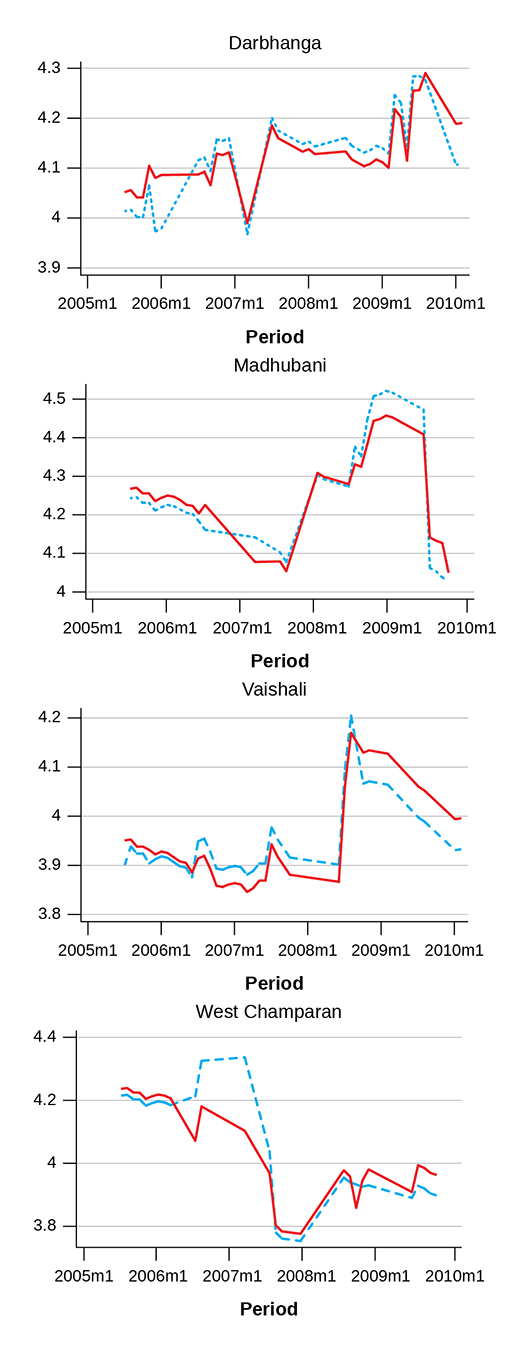
Figure 5D Two Estimates of Monthly Wages in Selected Districts of Bihar
In West Champaran, dotted and solid lines diverged substantially in the second agricultural year, suggesting the importance of controlling centre fixed effects. In both Madhubani and West Champaran, inter-year changes are smaller in solid lines (“FE_Control”). It appears that district specific factors spuriously create too much inter-year fluctuations. By controlling for centre-fixed effects, the inter-year fluctuations are suppressed.
Finally, in Figure 5E, two estimates for two selected districts in Andhra Pradesh are plotted. As already discussed and shown in Appendix Table 1, this State is exceptional in two aspects. First, as farm operations are not distinguished in the AWI report from the beginning, the issue of controlling operation fixed effects is absent. Secondly, in all districts, there is only one reporting centre for the first year and the last three years, while two more centres were added in the second year. Because of this homogeneity, the issue of centre fixed effects is also homogenous. For these reasons, we report only two districts as illustration.
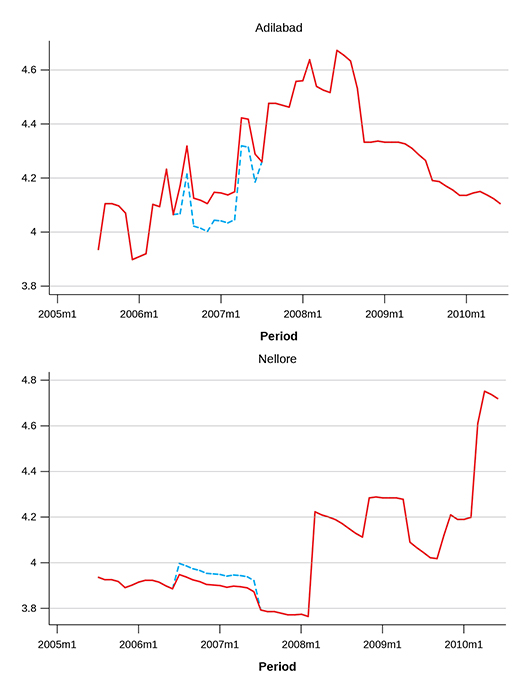
Figure 5E Two Estimates of Monthly Wages in Selected Districts of Andhra Pradesh
In Adilabad District, the “All_Avg” estimate (dotted line) shows a wage decrease in the second agricultural year, which disappears in the “FE_Control” estimate (solid line). Our interpretation is that because the additional centres in the second year had centre specific effects that were lower than the average, the “All_Avg” approach underestimated wage levels in the district in the second year. In Nellore District, on the other hand, the dotted line is above the solid line in the second agricultural year and the solid line connects years more smoothly. Our interpretation is that because the additional centres in the second year had centre specific effects that were higher than the average, the “All_Avg” approach overestimates wage levels in the district in the second year by about 5 per cent. Looking over all districts in Andhra Pradesh, we found that underestimation and overestimation occur with similar frequency.
4.4. Robustness Check
As a robustness check, we replace wagecdkt (natural log of real wages) in our model by (i) level instead of natural log, (ii) natural log of nominal wages instead of real wages, and (iii) the level of nominal wages. As expected, the results are highly similar regardless of the use of logs or levels (they are available on request from the authors). Our main result, i.e., that changes in reporting centres have a large impact on inter-year dynamics and changes in farm operations occasionally reverse the sign of monthly dynamics within a year so that the centre- and operation-specific effects need to be controlled by fixed effects, remains the same qualitatively. What is important is that when nominal wages are used instead of real wages, month-specific components became more significant in the ANOVA analysis. This is plausible, because nominal wages could change over months within an agricultural year because of inflation in addition to seasonal price variation.
In another check of robustness, we used weighted regressions/averages (instead of unweighted regressions/averages) in calculating the fixed effect controlled series, using the State-level weights for the differential importance of different farm operations, extracted from microdata in the 66th NSS data (2009–10) on employment. This is far from ideal as we would like to adjust for the different importance of different centres in a district as well, adjust at the district level regarding the farm operations, and to use weights that are time-varying. The weighted results are very similar to those reported in this article (they are available on request). If district-level and time-varying weights were used instead, the result could be different but such information is not available.
5. Conclusion
In this paper, we presented an overview of the limitations of AWI data and the causes of these limitations and then attempted to mitigate them by controlling for fixed effects associated with reporting centres and farm operations. It was found that centre and operation fixed effects were statistically significant, a naïve method of averaging over different centres and operations is likely to result in biased estimates for district-level monthly wages, and another naïve method of using only observations from the same centre and same farm operation suffers from too small a number of observations, due to missing data.
We thus proposed a way to utilise the AWI data as a source of district-level monthly wage variation without discarding districts with frequent missing data, by using a fixed effects approach. Our estimates, in which fixed effects were controlled, were found to perform better than the naïve estimates of simple averages. The two estimates differed widely, especially when reporting centres were changed across agricultural years. Furthermore, it was found that differences in farm operations for which data were collected sometimes spuriously reversed the direction of wage change between months within an agricultural year. In certain district-level analyses such evidence on monthly wage changes could bias empirical results seriously. Therefore, controlling for both fixed effects is necessary. However, our methodology does not work well if reporting centres are changed every year, as centre fixed effects are not clearly distinguished from annual trends. For this reason, keeping the same reporting centres across several years is necessary to improve the quality of AWI.
The main take-home message is that AWI data can be utilised as a rich source of district-level monthly wages if care is taken to recognise the non-random nature of missing data across centres and farm operations. When the district-level monthly wage is used as an explanatory variable in regression analysis, taking out the fixed effects of centres and farm operations is required before taking the district average for each month. When wages are used as the dependent variable in the regression analysis, district-level monthly wages distinguishing centres and operations can be used as they are, if the explanatory variables include centre and operation fixed effects.
The analysis in this paper is meant for illustrative purposes, covering a restricted number of States and years. The fixed effect approach proposed in this paper would become more powerful if applied to the AWI data covering a longer period than analysed here, because the changes in reporting centres/districts and changes in district boundaries become more frequent in such cases. Our fixed effect approach employs AWI data at the centre level so that changes in district boundaries do not matter much as long as we have precise information on the district (in a particular reference year) in which a centre is located. Although the focus of this article was on the informed use of a single wage data source (i.e., AWI), the fixed effect approach can be applied to combine wage data from two or more data sources by extending the regression model with another fixed effect for the data source. The practical utility of such analysis needs to be examined carefully. This is left for further research. Ultimately, fundamental determinants of wage variations, such as infrastructure and market development and rural development policies, ought to be examined. More structural and institutional understanding of what leads to missing data or distorted observations is also very much needed. By accumulating observations from the field on the reasons for missing data, our understanding of the AWI, and in particular of the conditions under which it is reliable and comparable, will be deepened. Research on such contextualising information can provide a valuable complement to this note.
Notes
1 Data on agricultural wages are also available in the Season and Crops Report (SCR) published by State governments. Rao (1972) and Ghanekar (1997) compared AWI data with SCR data. However, not all States publish SCR regularly and it is very difficult to collect all issues for a long period as SCR is a State government publication. Other sources of agricultural wages in India include those from the NSS (National Sample Surveys) compiled by the NSS Organisation and Wage Rates in Rural India (WRRI) reported by the Labour Bureau, Government of India. Rao (1972) compared AWI data with NSS data while Usami (2011) analysed WRRI data. WRRI began in 1986–87, limiting its usefulness for a long-term analysis.
4 From Appendix Table 1, we can calculate the number of districts for which we can obtain 5-year estimates based on the “Ope_Avg” approach. For Tamil Nadu, 0 out of 29; for Rajasthan, 5 out of 32; for Bihar, 4 out of 25, and for Andhra Pradesh, 17 out of 22. Andhra Pradesh is the only State out of the four where this approach appears useful.
5 The statistical significance of month specific effects in Rajasthan disappeared in the wage level regression, instead of log wage regression. Therefore, its significance is not robust.
6 These are much larger than the number of observations available under the “Ope_Avg” approach. See footnote 4 for a comparison.
References
| Berg, Erlend, Bhattacharyya, Sambit, Rajasekhar, Durgam, and Manjula, R. (2014), “Can Public Employment Schemes Increase Equilibrium Wages? Evidence from a Natural Experiment in India,” CMPO Working Paper No. 14/317, Centre for Market and Public Organisation, University of Bristol, Jan. | |
| Chavan, Pallavi and Bedamatta, Rajshree (2006), “Trends in Agricultural Wages in India, 1964–65 to 1999–2000,” Economic and Political Weekly, Sep. 23, pp. 4041–51. | |
| Directorate of Economics and Statistics (DES), Department of Agriculture and Cooperation, Ministry of Agriculture, Government of India, Agricultural Wages in India, various issues (also available at http://eands.dacnet.nic.in/AWIS.htm for the years 2005–6 to 2009–10). | |
| Ghanekar, Jayanti (1997), “Sorry State of Agricultural Wage Data Sources and Methods of Collection,” Economic and Political Weekly, May 10, pp. 1029–36. | |
| Himanshu (2005), “Wages in Rural India: Sources, Trends and Comparability,” The Indian Journal of Labour Economics, vol. 48, no. 2, pp. 375–406. | |
| Jose, A. V. (1988), “Agricultural Wages in India,” Economic and Political Weekly, Jun 25, pp. A46–58. | |
| Labour Bureau, Ministry of Labour and Employment, Government of India, Consumer Price Index Numbers for Agricultural and Rural Labourers, various issues. | |
| Rao, V. M. (1972), “Agricultural Wages in India: Reliability Analysis,” Indian Journal of Agricultural Economics, vol. 27, no. 3, pp. 38–62. | |
| Usami, Yoshifumi (2011), “A Note on Recent Trends in Wages in Rural India,” Review of Agrarian Studies, vol. 1, no. 1, pp. 149–82 (also available at http://www.ras.org.in/a_note_on_recent_trends_in_wage_rates_in_rural_india). |
Appendix Table 1 Data distribution across centres and agricultural years
| State/District1 | Centre | yr200506 | yr200607 | yr200708 | yr200809 | yr200910 |
| Tamil Nadu | ||||||
| Coimbatore* | Myleripalayam | 32 | 0 | 0 | 0 | 0 |
| Narasipuram | 0 | 0 | 26 | 32 | 42 | |
| Vellalore | 0 | 29 | 0 | 0 | 0 | |
| Cuddalore | Maruvai | 0 | 0 | 11 | 23 | 38 |
| Dharmapuri* | Annasagaram | 0 | 25 | 0 | 0 | 0 |
| Vellampatti | 12 | 0 | 37 | 50 | 44 | |
| Dindugul | Lekkayankottai | 35 | 0 | 0 | 0 | 0 |
| M.Pnajampatty | 0 | 0 | 11 | 11 | 37 | |
| Erode | Kanakampalayam | 0 | 0 | 23 | 29 | 49 |
| Kacheepuram* | Mannur SPR | 0 | 0 | 23 | 25 | 37 |
| Angampakkam KMP | 15 | 14 | 0 | 0 | 0 | |
| Kanniyakumari | Aruvikkarai | 0 | 0 | 19 | 3 | 16 |
| Karur* | Palaviduthi | 0 | 5 | 0 | 0 | 0 |
| Panchapatty | 11 | 0 | 0 | 0 | 0 | |
| Pannapatti | 0 | 0 | 9 | 8 | 23 | |
| Krishnagir | Vadamalampatti | 0 | 0 | 21 | 14 | 42 |
| Madurai | Katchirairuppu | 0 | 0 | 11 | 13 | 36 |
| Nagapatinam* | Kilaiyur | 0 | 0 | 11 | 24 | 30 |
| Pattavarthi | 0 | 17 | 0 | 0 | 0 | |
| Sikar | 18 | 0 | 0 | 0 | 0 | |
| Namakkal* | Mangalapuram | 0 | 0 | 15 | 29 | 33 |
| Porasalpatti | 8 | 11 | 0 | 0 | 0 | |
| Nilgiris | Thuneri | 0 | 0 | 33 | 8 | 38 |
| Perambalur | Silambur South | 0 | 0 | 14 | 16 | 22 |
| Pudukkottai | Kodumballur | 0 | 0 | 8 | 19 | 40 |
| Ramananthapuram* | Athiyoothu | 0 | 0 | 10 | 16 | 22 |
| Manjur | 17 | 14 | 0 | 0 | 0 | |
| Salem* | Aryapalayam | 0 | 0 | 36 | 36 | 50 |
| Kottavadi | 35 | 39 | 0 | 0 | 0 | |
| Sivagangai | Melachemponneri | 0 | 0 | 11 | 14 | 22 |
| Thanjavur | Veppathur 2 | 0 | 0 | 17 | 22 | 37 |
| Theni | Kullapuram | 0 | 0 | 27 | 35 | 40 |
| Thiruvallur* | Kalayanpur | 4 | 0 | 0 | 0 | 0 |
| Pedupettu | 0 | 0 | 12 | 21 | 26 | |
| Thamaraipakkam | 0 | 22 | 0 | 0 | 0 | |
| Thiruvarur* | Kandamangalam | 0 | 24 | 0 | 0 | 0 |
| Kottur | 27 | 0 | 0 | 0 | 0 | |
| Kurichi | 0 | 0 | 20 | 25 | 24 | |
| Thoothukudi | Kayathar | 0 | 0 | 10 | 16 | 20 |
| Tiruchirapalli | Perur | 0 | 0 | 13 | 18 | 31 |
| Tirunelveli* | Sundankurichi | 9 | 23 | 0 | 0 | 0 |
| Thuthikulam | 0 | 0 | 14 | 12 | 28 | |
| Tiruvannamalai* | Thurinjapuram | 12 | 0 | 11 | 19 | 40 |
| VP Kuppam | 0 | 23 | 0 | 0 | 0 | |
| Vellore* | Marasappali | 0 | 0 | 14 | 22 | 30 |
| Peddur | 16 | 0 | 0 | 0 | 0 | |
| Vandranthangal | 0 | 13 | 0 | 0 | 0 | |
| Villupuram* | Ganapathipattu | 15 | 0 | 0 | 0 | 0 |
| Naraiyur | 0 | 23 | 0 | 0 | 0 | |
| Semmanagur | 0 | 0 | 30 | 34 | 42 | |
| Virudhnaga | Pudukottai | 0 | 0 | 15 | 7 | 27 |
| Total of Tamil Nadu | 266 | 282 | 512 | 601 | 966 | |
| Rajasthan | ||||||
| Ajmer* | Dadiya | 0 | 0 | 17 | 7 | 9 |
| Khapra | 25 | 13 | 0 | 0 | 0 | |
| Alwar | Semlakhurd | 0 | 9 | 18 | 11 | 9 |
| Banswara | Ajana | 0 | 0 | 24 | 24 | 19 |
| Baren* | Dhothi | 32 | 7 | 9 | 11 | 15 |
| Barmer | Vishla | 0 | 0 | 3 | 2 | 10 |
| Bharatpur | Jaghina | 0 | 0 | 8 | 5 | 7 |
| Jaghina | 0 | 0 | 8 | 5 | 7 | |
| Khanua | 0 | 10 | 0 | 0 | 0 | |
| Bhilwara* | Asind | 1 | 0 | 0 | 0 | 0 |
| Bigod | 0 | 40 | 36 | 36 | 17 | |
| Bikaner | Nathusar | 0 | 0 | 0 | 0 | 4 |
| Bundi* | Daulara | 17 | 18 | 6 | 21 | 16 |
| Chittorgarh | Adhana | 0 | 6 | 4 | 16 | 11 |
| Churu | Jasrasar | 0 | 0 | 0 | 0 | 2 |
| Dausa | Didwana | 0 | 7 | 4 | 1 | 5 |
| Dholpur | Hathwari | 0 | 8 | 1 | 12 | 7 |
| Dungerpur | Karada | 0 | 0 | 8 | 0 | 0 |
| Ganganagar | Sllg | 0 | 0 | 0 | 19 | 17 |
| Hanumangarh | Dhulwana | 3 | 0 | 0 | 0 | 0 |
| Sggr | 0 | 0 | 10 | 7 | 13 | |
| Jaipur | Chitanukalan | 0 | 4 | 0 | 0 | 0 |
| Neendar | 0 | 0 | 9 | 8 | 4 | |
| Jaisalmer | Bhairuda | 0 | 0 | 0 | 0 | 4 |
| Jalore | Sayala | 0 | 0 | 20 | 36 | 14 |
| Jhalawar | Bani | 0 | 2 | 6 | 6 | 9 |
| Jhunjhunu | Bajawa | 0 | 31 | 39 | 47 | 28 |
| Jodhpur | Sekhala | 5 | 0 | 1 | 0 | 2 |
| Karauli | Nadoti | 0 | 20 | 15 | 10 | 10 |
| Kota | Sitalkheri | 0 | 10 | 8 | 24 | 26 |
| Madhopur | Meenapara | 0 | 12 | 0 | 0 | 14 |
| Nagaur | Jayal | 3 | 0 | 0 | 0 | 5 |
| Pali* | Dayalnakalan | 8 | 6 | 5 | 10 | 7 |
| Rajsamand | Mohi | 0 | 0 | 5 | 12 | 12 |
| Sikar | Nathusar | 0 | 1 | 3 | 3 | 7 |
| Sirohi* | Manora | 43 | 20 | 28 | 32 | 30 |
| Tonk* | Amli | 10 | 5 | 7 | 3 | 6 |
| Sohela | 0 | 3 | 0 | 0 | 0 | |
| Udaipur* | Peepli | 0 | 0 | 20 | 24 | 30 |
| Sare | 1 | 2 | 0 | 0 | 0 | |
| Total of Rajasthan | 429 | 552 | 879 | 1034 | 1411 | |
| Bihar | ||||||
| Aurangabad | Hasauli | 14 | 24 | 2 | 0 | 0 |
| Banka | Bharkohat | 20 | 0 | 0 | 0 | 0 |
| Begusarai | Simariya | 0 | 0 | 0 | 1 | 0 |
| Bhagalpur | Dharhara | 0 | 0 | 0 | 6 | 0 |
| Bhojpur | Kadara | 0 | 6 | 0 | 0 | 0 |
| Darbhanga* | Godhail | 21 | 1 | 0 | 0 | 4 |
| Sirniya | 15 | 18 | 5 | 42 | 9 | |
| East Champaran | Jhajhara | 37 | 3 | 0 | 0 | 0 |
| Wariyarpur | 0 | 3 | 0 | 0 | 0 | |
| Gaya | Karchoe | 0 | 2 | 0 | 22 | 0 |
| Turi | 0 | 6 | 10 | 12 | 8 | |
| Jamui | Goddi | 4 | 7 | 0 | 0 | 0 |
| Jehanabad | Bara | 29 | 34 | 1 | 0 | 0 |
| Madhubani* | Bhakharaen | 0 | 1 | 0 | 0 | 6 |
| Parasa | 33 | 2 | 0 | 0 | 0 | |
| Radhakant | 0 | 3 | 15 | 20 | 7 | |
| Monghyr | Nauvagarhi | 10 | 7 | 6 | 31 | 0 |
| Muzaffarpur* | Bhalui Rasool | 3 | 6 | 6 | 27 | 12 |
| Nalanda | Diyawan | 22 | 1 | 2 | 0 | 0 |
| Nawada | Masai | 44 | 8 | 15 | 21 | 0 |
| Patna | Dighwa Manadevpur | 12 | 0 | 0 | 0 | 0 |
| Maujipur | 0 | 7 | 0 | 0 | 0 | |
| Purnia | Machchhanata | 0 | 1 | 3 | 22 | 4 |
| Rohtas | Mokar | 9 | 0 | 0 | 0 | 0 |
| Samastipur | Brijmainiya | 0 | 36 | 0 | 0 | 0 |
| Chandauli | 0 | 5 | 0 | 39 | 0 | |
| Ujiyarpur | 0 | 5 | 0 | 0 | 0 | |
| Shekhpura | Kutaut | 0 | 9 | 5 | 5 | 5 |
| Sheohar | Narayanpur | 0 | 0 | 0 | 3 | 0 |
| Sitamarhi | Bela | 0 | 0 | 0 | 34 | 3 |
| Majhauliya | 0 | 0 | 0 | 9 | 0 | |
| Supaul | Dagmara | 0 | 0 | 7 | 4 | 0 |
| Sukhapur | 0 | 0 | 2 | 9 | 0 | |
| Vaishali* | Radhopur Chaturang | 26 | 12 | 4 | 5 | 4 |
| West Champaran* | Jhakhauli | 27 | 3 | 16 | 19 | 8 |
| Pakari | 0 | 10 | 3 | 2 | 0 | |
| Total of Bihar | 326 | 220 | 102 | 333 | 70 | |
| Andhra Pradesh | ||||||
| Adilabad* | Basar | 11 | 12 | 12 | 12 | 12 |
| Khaperla | 0 | 12 | 0 | 0 | 0 | |
| Sarangapur | 0 | 12 | 0 | 0 | 0 | |
| Anantapur* | Bukkapatinam | 12 | 11 | 11 | 12 | 12 |
| Kanekal | 0 | 12 | 0 | 0 | 0 | |
| Taluputa | 0 | 12 | 0 | 0 | 0 | |
| Chittoor* | Gollapali | 12 | 12 | 12 | 12 | 12 |
| PTM | 0 | 12 | 0 | 0 | 0 | |
| Thondamanadu | 0 | 12 | 0 | 0 | 0 | |
| Cuddapah | Chinur | 0 | 12 | 12 | 12 | 11 |
| Chitvel | 0 | 12 | 0 | 0 | 0 | |
| Duvvur | 0 | 12 | 0 | 0 | 0 | |
| East Godavari* | Katravulapalli | 0 | 12 | 0 | 0 | 0 |
| Kothapalli | 12 | 11 | 12 | 12 | 12 | |
| Yditta | 0 | 12 | 0 | 0 | 0 | |
| Guntur | Amaravati | 0 | 12 | 0 | 0 | 0 |
| Nizapatnam | 0 | 12 | 12 | 12 | 12 | |
| Veldurthi | 0 | 12 | 0 | 0 | 0 | |
| Karimnagar* | Cheppail | 12 | 12 | 12 | 12 | 12 |
| Kadurpak | 0 | 12 | 0 | 0 | 0 | |
| Tadicherla | 0 | 12 | 0 | 0 | 0 | |
| Khammam* | Chennaram | 0 | 11 | 0 | 0 | 0 |
| Cherla | 12 | 12 | 12 | 12 | 12 | |
| Gundepadi | 0 | 12 | 0 | 0 | 0 | |
| Krishna | Ibrahimpatnam | 0 | 11 | 0 | 0 | 0 |
| Pamarru | 0 | 12 | 12 | 12 | 12 | |
| Vissannapet | 0 | 11 | 0 | 0 | 0 | |
| Kurnool* | Sirvel | 12 | 12 | 12 | 12 | 12 |
| Veldurthy | 0 | 11 | 0 | 0 | 0 | |
| Yammiganur | 0 | 12 | 0 | 0 | 0 | |
| Medak* | Ramayampet | 0 | 12 | 0 | 0 | 0 |
| Sanga Reddy | 12 | 12 | 12 | 12 | 12 | |
| Siddipet | 0 | 12 | 0 | 0 | 0 | |
| Mahabubnagar* | Bijhapally | 0 | 12 | 0 | 0 | 0 |
| Veldanda | 12 | 12 | 12 | 12 | 12 | |
| Waddenapalli | 0 | 11 | 0 | 0 | 0 | |
| Nalgonda* | Atmakur | 12 | 12 | 11 | 11 | 12 |
| Huzurnagar | 0 | 12 | 0 | 0 | 0 | |
| Kethepally | 0 | 12 | 0 | 0 | 0 | |
| Nellore* | Indukurpet | 0 | 12 | 0 | 0 | 0 |
| Marripadu | 0 | 12 | 0 | 0 | 0 | |
| Tummur | 12 | 12 | 12 | 12 | 12 | |
| Nizamabad* | Chandoor | 12 | 12 | 12 | 12 | 12 |
| Madnoor | 0 | 12 | 0 | 0 | 0 | |
| Yadpalli | 0 | 8 | 0 | 0 | 0 | |
| Prakasam* | Buddavanipalem | 0 | 8 | 0 | 0 | 0 |
| Chapalamadugu | 0 | 8 | 0 | 0 | 0 | |
| Karanchedu | 12 | 10 | 11 | 12 | 10 | |
| Rangareddy | Medchal | 0 | 12 | 12 | 12 | 12 |
| Mominpet | 0 | 12 | 0 | 0 | 0 | |
| Pargi | 0 | 12 | 0 | 0 | 0 | |
| Srikakulam* | Baruva | 0 | 12 | 0 | 0 | 0 |
| Korasawada | 12 | 12 | 12 | 12 | 12 | |
| Nadgram | 0 | 12 | 0 | 0 | 0 | |
| Visakhapatanam | Ponugallu | 0 | 12 | 12 | 12 | 10 |
| Ravikamatham | 0 | 12 | 0 | 0 | 0 | |
| Vaddadi | 0 | 12 | 0 | 0 | 0 | |
| Vizianagaram* | Bonangi | 12 | 12 | 12 | 12 | 12 |
| Dalaipeta | 0 | 12 | 0 | 0 | 0 | |
| Peddpenki | 0 | 12 | 0 | 0 | 0 | |
| Warangal* | Anantharam | 0 | 12 | 0 | 0 | 0 |
| Chagallu | 12 | 12 | 12 | 11 | 12 | |
| Incherla | 0 | 12 | 0 | 0 | 0 | |
| West Godavari* | Bheemadolu | 0 | 12 | 0 | 0 | 0 |
| Koyyalagudem | 12 | 12 | 12 | 12 | 12 | |
| Veeravasaran | 0 | 12 | 0 | 0 | 0 | |
| Total of Andhra Pradesh | 203 | 771 | 261 | 262 | 259 |
Note: 1 Districts where data exist for all five years (subject to some missing months) are denoted with an asterisk (*).
Appendix Table 2 Data distribution across farm operations and time periods
| (Actual name in AWI) | Agricultural years | |||||
| 2005–06 | 2006–07 | 2007–08 | 2008–09 | 2009–10 | ||
| Tamil Nadu | ||||||
| Ploughing | (Ploughman) | 45 | 75 | 66 | 75 | 111 |
| Sowing | (Sower) | 41 | 48 | 64 | 99 | 173 |
| Weeding | (Weeder) | 1 | 8 | 33 | 53 | 109 |
| Harvesting | (Harvester) | 77 | 88 | 196 | 166 | 270 |
| Non-specified | (Other agricultural labour) | 102 | 63 | 153 | 208 | 303 |
| Rajasthan | ||||||
| Ploughing | (Ploughman) | 38 | 62 | 94 | 110 | 101 |
| Sowing | (Sower) | 37 | 53 | 81 | 101 | 83 |
| Weeding | (Weeder) | 42 | 62 | 64 | 91 | 99 |
| Harvesting | (Harvester) | 31 | 57 | 75 | 85 | 86 |
| Bihar | ||||||
| Ploughing | (Ploughman) | 114 | 72 | 21 | 96 | 4 |
| Sowing | (Sower) | 66 | 54 | 42 | 79 | 36 |
| Weeding | (Weeder) | 90 | 50 | 29 | 79 | 27 |
| Harvesting | (Reaper) | 56 | 44 | 10 | 79 | 3 |
| Andhra Pradesh | ||||||
| Non-specified | (Field labour) | 203 | 771 | 261 | 262 | 259 |
| Months within an agricultural year | ||||||||||||
| m01jul | m02aug | m03sep | m04oct | m05nov | m06dec | m07jan | m08feb | m09mar | m10apr | m11may | m12jun | |
| Tamil Nadu | ||||||||||||
| Ploughing | 36 | 35 | 38 | 36 | 35 | 30 | 26 | 31 | 26 | 21 | 25 | 33 |
| Sowing | 42 | 47 | 47 | 45 | 37 | 26 | 33 | 34 | 22 | 25 | 34 | 33 |
| Weeding | 15 | 15 | 16 | 16 | 20 | 16 | 14 | 16 | 24 | 17 | 22 | 13 |
| Harvesting | 62 | 64 | 59 | 52 | 56 | 69 | 89 | 91 | 72 | 61 | 66 | 56 |
| Non-specified | 68 | 72 | 79 | 66 | 66 | 69 | 70 | 68 | 70 | 65 | 72 | 64 |
| Rajasthan | ||||||||||||
| Ploughing | 41 | 37 | 31 | 36 | 42 | 37 | 26 | 29 | 19 | 30 | 37 | 40 |
| Sowing | 43 | 31 | 20 | 27 | 44 | 38 | 24 | 25 | 17 | 23 | 28 | 35 |
| Weeding | 38 | 41 | 38 | 28 | 32 | 44 | 26 | 28 | 16 | 22 | 21 | 24 |
| Harvesting | 13 | 19 | 38 | 34 | 30 | 25 | 21 | 42 | 29 | 38 | 25 | 20 |
| Bihar | ||||||||||||
| Ploughing | 54 | 43 | 31 | 28 | 25 | 20 | 17 | 15 | 26 | 16 | 15 | 17 |
| Sowing | 54 | 43 | 28 | 25 | 23 | 18 | 20 | 17 | 16 | 10 | 10 | 13 |
| Weeding | 49 | 45 | 29 | 24 | 20 | 17 | 19 | 16 | 20 | 12 | 12 | 12 |
| Harvesting | 27 | 23 | 16 | 17 | 20 | 16 | 12 | 11 | 21 | 11 | 9 | 9 |
| Andhra Pradesh | ||||||||||||
| Non-specified | 149 | 148 | 149 | 149 | 149 | 145 | 147 | 149 | 144 | 145 | 143 | 139 |


