ARCHIVE
Vol. 8, No. 2
JULY-DECEMBER, 2018
Introduction
Research Articles
Research Notes and Statistics
Conference
Obituary
Book Reviews
Referees
Covariates of Rural Female Work Participation:
A Study of the Hill Region of Darjeeling District
in West Bengal, India
*Assistant Professor, Department of Economics, Kurseong College, srijanarai2001@yahoo.com
†Professor, Department of Economics, University of North Bengal, sancharirm@gmail.com
Abstract: Women’s labour market decisions depend greatly on decisions taken at the household level. These decisions in turn are determined by social, economic, demographic, personal, religious, and cultural factors. This study investigates and identifies the covariates of rural female work participation using primary survey data from 2016–17 for three villages in the hill region of Darjeeling district (including Kalimpong sub-division) in the State of West Bengal. Based on a sample of 235 rural women, the study estimates two models using logistic regression analysis. We observe that women’s participation in paid activities is significantly and positively related to the level of education, and significantly and negatively related to joint family structure, the presence of children below the age of six, and the extent of household landholding. For both paid and unpaid work on family farms, we observe that age has a non-linear effect on women’s participation. Women belonging to a unitary family structure and agricultural households are more likely to participate in paid and unpaid work as family labour, controlling for other variables.
Keywords: Female work participation, rural, hill districts, paid work, unpaid work, covariates, West Bengal, Darjeeling.
Introduction
Women’s decision to participate in the labour market and the nature of work in which they are engaged are influenced by decisions taken at the household level and depend on several factors. The members of a family divide among themselves paid work, unpaid housework (including cooking, cleaning, and washing), and care work (care of small children and the elderly) to suit household requirements. This division of work depends on a variety of factors, such as individual beliefs about appropriate gender roles and child-rearing practices, as well as perceptions about the value of women’s contribution. These perceptions in turn are influenced and shaped by the relative bargaining power of household members, which are affected by potential income, human capital, economic dependency, potential status of employment, as well as specific household needs and interests (ILO 2012, p. 35).
Despite significant contributions to the functioning of an economy, the female labour force in less-developed countries continues to be neglected and underutilised, making it a socially and economically disadvantaged human resource. This has obvious implications for economic welfare and growth (Psacharopoulos and Tzannatos 1989).
The attitude of society . . . towards what constitutes woman's work and her place in society . . . held not only by men but by women themselves and reflected in national data systems, exclude large numbers from the estimation of the workforce and consider them to be non-employed, not wishing to participate in the labour market (Sundar 1981).
The underestimation of women’s work is a result of women’s relatively high involvement in unpaid work, which lacks visibility. “Since status in contemporary society is so often equated with income-earning power, women suffer a major undervaluation of their economic status” (UNDP 1995, p. 6). “Within the family” it “determines the hierarchy in gender relations . . . and acts as the mainspring of gender inequalities” (ActionAid 2017, p. 15). Agarwal (1997) notes that the debate within Western feminism on “wages for housework” was based on the recognition that unpaid work was “invisible” and perceived as “possessing little value.” England and Kilbourne (1990) use studies of American households to argue that women who earn have greater bargaining power than women who are solely housewives, because of, among other things, the cultural devaluation of housework (Agarwal 1997). Women’s entry into wage labour is thus one way of increasing intra-family bargaining power, not only directly, but also by increasing the perceived legitimacy of their claims (ibid.; see also Sen 1990).
The participation of women in paid work, however, may not always be empowering. Chakraborty and Chakraborty (2009) point out that increased labour force participation by women as a response to economic stress may lead to young girls dropping out of school and being put to work at domestic chores and sibling care; the burden of work imposed on girls early in life may restrict their schooling, which in turn widens the gender gap in education and the gap in labour market opportunities. This implies that women may be employed in jobs that are of lower productivity and casual in nature (that is, not in regular contracts). Gender roles within the household thus translate into gender stratification in the labour market.
Participation of women in the labour force is a function of a wide range of factors, among which non-economic factors are also significant. Women’s involvement in paid work is determined by factors as diverse as demographic, reproductive, social, religious, cultural, and personal factors (Sundar 1981; Srivastava and Srivastava 2010). There is considerable heterogeneity in female labour force participation rates across regions and nations. Standing (1981) observes that “any generalisation about female labour force participation is liable to be misleading, since level, patterns, and trends vary widely between and within countries” (op. cit. Psacharopoulos and Tzannatos 1989). Female labour force participation thus requires analysis within the socio-economic and demographic context of the area under study.
Research on the relatively high work participation rates of women in the hill and mountain regions of India is somewhat limited. According to the 2011 Census, the rural female work participation rate for the hill district of Darjeeling (including Kalimpong sub-division) in the State of West Bengal was 26 per cent, which was the third highest among all districts of the State and higher than the State average of 19.4 per cent. Lack of caste-specific occupational specialisation, higher cost of living, and low productivity of land have been identified as some of the reasons for the high rate of work participation in Darjeeling district as compared to other districts in West Bengal (Subba 1985, p. 20). The gender division of labour, which is weaker in highland areas, may also contribute to high female work participation in Darjeeling district. Agricultural activities in the hill regions are often conducted for subsistence and are distinctly different from those practised in lowland areas, due to limitations imposed by altitude and topography. In such settings, women’s participation in economic activities is affected by several factors that have received little attention from scholars. Keeping this in mind, the present study examines the contribution of rural women in the hill region in Darjeeling district (including Kalimpong sub-division) in the State of West Bengal, by taking into account paid work and unpaid work in family farms, and identifying the determinants of work participation.
Study Area, Data, and Characteristics of the Study Villages
The study examines the determinants of work participation for women in the rural hill regions of West Bengal. It is based entirely on primary data collected as part of a survey conducted in hill regions of Darjeeling district (including Kalimpong sub-division) in 2016–17. Kalimpong was accorded the status of a district only on February 14, 2017, and was therefore a sub-division of Darjeeling district at the time of survey.
The former district of Darjeeling comprised four sub-divisions: Darjeeling Sadar, Kurseong, Kalimpong, and Siliguri. The first three of these sub-divisions are in the hill areas and the fourth is in the plains. Siliguri sub-division is excluded from the present study as it is not a hill area. Among the three hill sub-divisions of Darjeeling district, Darjeeling Sadar and Kalimpong (now a district) had three community development blocks each, and Kurseong sub-division had two community development blocks. For purposes of the survey, one community development block each, with a higher-than-average proportion of agricultural workers, was chosen from the sub-divisions of Darjeeling Sadar and Kalimpong, and Kurseong block was chosen from Kurseong sub-division because of its proximity to the town. The village with a relatively high proportion of agricultural workers was selected randomly from each block. The villages selected for the survey were Samalbong in Darjeeling Sadar, Git Dubling Khasmahal in Kalimpong, and Sitong Khasmahal in Kurseong.1
Table 1 shows the socio-economic and demographic characteristics of the three sample villages. The villages are primarily agrarian in character. While 70 per cent of heads of household reported agriculture as their primary activity in Git Dubling Khasmahal village, the corresponding proportions in Samalbong and Sitong Khasmahal were lower, at 38 and 44 per cent respectively. Table 2 shows the structure of female employment (usual primary activity status) in the three sample villages. It is clear that among economically active women, the proportion of women involved in agriculture was higher than those engaged in non-agricultural activities, with agricultural workers displaying a higher proportion of self-employed. The labour exchange system of “parma” that exists in some of the hill areas is a major reason for the low percentage of agricultural workers.2 Non-agricultural activities in the villages included petty trade, working in government offices, as mid-day meal cooks, as Integrated Child Development Services (ICDS) scheme helpers, and in teaching. The principal crops in the villages were black cardamom, broom grass, potato, round red chilli, seasonal vegetables such as squash, beans, green leafy vegetables, and maize, rice, and pulses at lower altitudes. Livestock-rearing was an important aspect of mountain farming, and primarily served as a source of manure. It also supplemented family income, especially in times of distress.
Table 1 Socio-economic and demographic characteristics of sample villages, 2016–17
| Village | Samalbong | Git Dubling Khasmahal | Sitong Khasmahal |
| A. Demographic factors | |||
| 1. Population | |||
| Males | 117 | 127 | 128 |
| Females | 113 | 108 | 136 |
| 2. Age | |||
| Mean age of men | 30.7 | 32.6 | 34.1 |
| Mean age of women | 30.7 | 37 | 33.8 |
| B. Social factors | |||
| 1. Family structure | |||
| Unitary family (percentage) | 68 | 54 | 32 |
| Joint family (percentage) | 32 | 46 | 68 |
| Average number of children (0–6 years) | 0.9 | 1 | 0.66 |
| 2. Literacy | |||
| Male literacy | 88.3 | 94.1 | 95 |
| Female literacy | 83 | 86.7 | 85.2 |
| 3. Marital status | |||
| Married males | 59.1 | 70.7 | 54.7 |
| Married females | 62.6 | 71.7 | 52.9 |
| C. Economic factors | |||
| 1. Primary activity of household heads | |||
| Agriculture (per cent) | 38 | 70 | 44 |
| Non-agriculture (per cent) | 62 | 30 | 56 |
| 2. Labour force characteristics | |||
| Work participation rate of males | 51 | 59.8 | 56.3 |
| Work participation rate of females | 41.6 | 52.8 | 47.8 |
| 3. Landholding of households | |||
| Average landholding (acres) | 1.4 | 2.8 | 1.7 |
| 4. Monthly income of households | |||
| Average monthly income (Rs) | 11,347 | 22,814 | 15,860 |
Source: Primary survey data.
Table 2 Usual principal activity status of women in the study villages, by type of employment, 2016–17 in number and per cent
| Activity | Samalbong | Git Dubling Khasmahal | Sitong Khasmahal | All | ||||||
| No. | % | No. | % | No. | % | No. | % | |||
| Agriculture, of which | 34 | 72.3 | 47 | 82.5 | 57 | 87.7 | 138 | 81.7 | ||
| 1 | Self-employed | 32 | 94.1 | 47 | 100 | 56 | 98.2 | 135 | 97.8 | |
| 2 | Agricultural labour | 2 | 5.9 | 0 | 0 | 1 | 1.8 | 3 | 2.2 | |
| 3 | Allied activities | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Non-agriculture, of which | 13 | 27.7 | 10 | 17.5 | 8 | 12.3 | 31 | 18.3 | ||
| 1 | Self-employed | 4 | 30.8 | 4 | 40 | 3 | 37.5 | 11 | 35.5 | |
| 2 | Regular wage/salaried | 9 | 69.2 | 6 | 60 | 5 | 62.5 | 20 | 64.5 | |
| 3 | Casual | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Total (Agriculture+Non-agriculture) | 47 | 100 | 57 | 100 | 65 | 100 | 169 | 100 | ||
Source: Primary survey data.
Fifty households were surveyed in each village. Information was collected through in-depth interviews of female respondents. The respondents were asked about the activities in which female members of the households, including themselves, participated. Information on other socio-demographic characteristics of the households was also collected. Only women between the ages of 15 and 65 were considered for the analysis, irrespective of whether or not they participated in an economic activity. Females attending educational institutions were excluded from the analysis. The total sample size was 235 (68 in Samalbong village, 74 in Git Dubling Khasmahal, and 93 in Sitong Khasmahal). The data were analysed using Statistical Package for the Social Sciences (SPSS) version 23 and Econometric Views (EViews) version 10.
The Employment and Unemployment Survey of the National Sample Survey Organisation (NSSO), 68th Round, defines economic activity as “any activity resulting in production of goods and services that add value to national product,” and includes activities such as “(i) production of all goods and services for the market (i.e. for pay or profit) including government services, (ii) production of primary commodities for own consumption, and (iii) own account production of fixed assets” (GoI 2013). Further, an activity on which a person spent a relatively long period of time (i.e. major time criterion) during the 365 days preceding the date of survey is considered as the usual principal activity status of the person, whereas the status in which an economic activity was pursued for a relatively shorter time, amounting to not less than 30 days during the reference year, is the subsidiary economic activity status. In the present study, the work participation of women is based only on usual principal activity status, i.e. a woman is said to be in the workforce according to the usual status (primary activity status) if she participates in any kind of activity for the major part of the 365 days preceding the survey. Women who are primarily engaged in household work and participate in economic activities on usual subsidiary activity status are considered to be outside the workforce. Unemployed women are not included in the workforce. The workforce therefore includes women in paid employment and those who work as unpaid family labour on family farms.
Following Ackah et al. (2009), two alternative models have been estimated in the present analysis on the basis of female workforce participation. Model I takes into consideration both paid and unpaid employment of women as participation in the workforce. It includes women in paid/wage work or self-employment, as well as those engaged in family farms as unpaid family labour. In order to arrive at the determinants of women’s paid work, Model II considers a more restrictive definition of participation that includes only paid market work, but covers both wage work and self-employment. Paid market work may be distinguished from unpaid work as “work that is remunerated in cash or kind in the shape of wages, salaries, and profit” whereas unpaid work is work “performed without any direct remuneration” (ActionAid 2017, p. 13).
Table 3 shows that out of 235 working-age women, 169 (71.9 per cent) participated in economic activities. Model I includes these 169 women. Model II, which takes into account only paid activities of women, includes only 34 women (14.5 per cent) who participated in paid economic activities.
Table 3 Frequency table for the binary response variable (Model I dependent variable – FLFP and Model II dependent variable – FLFP_PAID)
| Frequency | Percentage | Valid percentage | Cumulative percentage | ||
| Model I | |||||
| Valid | FLFP=0 | 66 | 28.1 | 28.1 | 28.1 |
| FLFP=1 | 169 | 71.9 | 71.9 | 100 | |
| Total | 235 | 100 | 100 | ||
| Model II | |||||
| Valid | FLFP_PAID=0 | 201 | 85.5 | 85.5 | 85.5 |
| FLFP_PAID=1 | 34 | 14.5 | 14.5 | 100 | |
| Total | 235 | 100 | 100 | ||
Notes: (i) FLFP is defined as paid work and unpaid work on family farms.
(ii) FLFP_PAID is paid market work, or work that is remunerated in cash or kind in terms of wages, salaries, and profit. It includes both wage work and self-employment.
Methodology
Variables Used in the Binary Logistic Regression Model
A review of the literature shows that various socio-economic variables influence the work participation behaviour of women. Table 4 lists the explanatory variables chosen for analysis along with the expected sign. Age squared has been used to capture the non-linear effect of age. It is, however, very likely that the age and age-squared terms are highly correlated.3 In the present analysis, age has been centred to reduce multicollinearity. The monthly per capita consumption expenditure of the household has been used as a proxy for household income to avoid the problem of endogeneity in the model. The expenditure incurred by a household on domestic consumption during the reference period is taken as the household’s consumption expenditure (GoI 2014, p. 8). In the present model, household expenditure on food items was estimated per month. For self-produced items such as vegetables and milk, the quantity consumed per month was recorded and the value estimated according to the prevailing market price. Expenditure on other items such as clothing, education, and agricultural inputs was estimated using a one-year recall period. Recall errors are an inherent limitation of the present study. We measured household monthly per capita consumption expenditure (MPCE) as a continuous variable in thousand rupees.
Table 4 Variables used in the model
| Variable | Notation | Description | Expected sign |
| Dependent variable | |||
| Model I: Female work participation | FLFP | Dummy variable =1 if participating in the workforce =0 otherwise | |
| Model II: Female work participation in paid work | FLFP_PAID | Dummy variable =1 if participating in the paid workforce =0 otherwise | |
| Independent variables | |||
| Age | AGE | Number of years completed | Positive |
| Age squared | AGE_SQU | Square of the number of years completed | Negative |
| Education | EDUCATION | Number of years of schooling | Positive |
| Family structure | FAM_STR | Dummy variable =1 joint = 0 unitary | Positive/Negative |
| Number of children below the age of six | CHILD_06 | Dummy variable =1 if child below the age of six years is present = 0 otherwise | Negative |
| Woman’s marital status | MARITAL_STATUS | Dummy variable=1 if currently married =0 otherwise | Negative |
| Primary occupation of household head | OCCUPATION_HEAD | Dummy variable=1 if primary occupation is agriculture =0 otherwise | Positive |
| Presence of male migrant member | MIGRANT | Dummy variable=1 if migrant male member is present =0 otherwise | Positive/Negative |
| Monthly per capita consumption expenditure | MPCE | Monthly per capita consumption expenditure of household in Rs 1,000 | Negative |
| Landholding | LAND | Ownership holding of household in acres | Positive/Negative |
Details of the specifications of the logistic regression model, the selection of variables, and the results from the analysis of the data are in the Appendix.
Results from the Logistic Regression
The p-values of the Wald statistics in Table 5 show that the variables that are significant in explaining female labour force participation as per Model I are AGE, AGE_SQU, FAM_STR, and OCCUPATION_HEAD.
Table 5 Binomial logistic regression estimates for female work participation – Model I
| Variables in the equation – Model I | |||||||||
| B | S.E. | Wald | df | Sig. | Exp(B) | 95 per cent C. I. for EXP(B) | |||
| Lower | Upper | ||||||||
| Step 1a | AGE | 0.104 | 0.021 | 24.884 | 1 | 0.000* | 1.109 | 1.065 | 1.155 |
| AGE_SQU | −0.006 | 0.001 | 23.323 | 1 | 0.000* | 0.994 | 0.991 | 0.996 | |
| EDUCATION | −0.034 | 0.041 | 0.702 | 1 | 0.402 | 0.966 | 0.891 | 1.047 | |
| FAMILY_STR(1) | −0.696 | 0.394 | 3.122 | 1 | 0.077*** | 0.498 | 0.230 | 1.079 | |
| CHILD_06(1) | −0.511 | 0.496 | 1.062 | 1 | 0.303 | 0.600 | 0.227 | 1.586 | |
| MARITAL_STATUS(1) | 0.619 | 0.445 | 1.938 | 1 | 0.164 | 1.857 | 0.777 | 4.441 | |
| OCCUPATION_HEAD(1) | 0.942 | 0.385 | 5.980 | 1 | 0.014** | 2.566 | 1.206 | 5.459 | |
| MIGRANT(1) | −0.358 | 0.447 | 0.639 | 1 | 0.424 | 0.699 | 0.291 | 1.681 | |
| Constant | 1.850 | 0.587 | 9.948 | 1 | 0.002** | 6.361 | |||
Notes: * significant at α = 0.001, ** significant at α = 0.050, and *** significant at α = 0.100.
Variable(s) entered for step 1: AGE, AGE_SQU, EDUCATION, FAM_STR, CHILD_06, MARITAL_STATUS, OCCUPATION_HEAD, MIGRANT
The variables that are significant in explaining women’s work participation in paid activities (Model II) are EDUCATION, FAM_STR, CHILD_06, and LAND (Table 6).
Table 6 Binomial logistic regression estimates for female work participation – Model II
| Variables in the equation | |||||||||
| B | S. E. | Wald | df | Sig. | Exp(B) | 95 per cent C. I. for EXP(B) | |||
| Lower | Upper | ||||||||
| Step 1a | AGE | 0.001 | 0.027 | 0.001 | 1 | 0.973 | 1.001 | 0.950 | 1.055 |
| AGE_SQU | −0.003 | 0.002 | 1.928 | 1 | 0.165 | 0.997 | 0.993 | 1.001 | |
| EDUCATION | 0.121 | 0.048 | 6.362 | 1 | 0.012** | 1.129 | 1.027 | 1.241 | |
| FAMILY_STR(1) | −0.938 | 0.458 | 4.185 | 1 | 0.041** | 0.392 | 0.159 | 0.961 | |
| CHILD_06(1) | −2.165 | 1.075 | 4.059 | 1 | 0.044** | 0.115 | 0.014 | 0.943 | |
| MARITAL_STATUS(1) | −0.636 | 0.511 | 1.546 | 1 | 0.214 | 0.530 | 0.194 | 1.443 | |
| OCCUPATION_HEAD(1) | −0.608 | 0.435 | 1.955 | 1 | 0.162 | 0.545 | 0.232 | 1.276 | |
| MIGRANT(1) | −0.983 | 0.667 | 2.176 | 1 | 0.140 | 0.374 | 0.101 | 1.382 | |
| LAND | −0.755 | 0.278 | 7.409 | 1 | 0.006** | 0.470 | 0.273 | 0.809 | |
| Constant | 0.353 | 0.687 | 0.263 | 1 | 0.608 | 1.423 | |||
Notes: ** significant at α = 0.050.
Variable(s) entered on step 1: AGE, AGE_SQU, EDUCATION, FAM_STR, MARITAL_STATUS, OCCUPATION_HEAD, MIGRANT, LAND.
Interpretation of the Results
Scholars have cited age as an important determinant of female participation in the workforce. Due to simultaneous demands made by children and at work, participation by women in the workforce during periods of child-bearing and child-rearing is likely to be lower than that of older women who are beyond this age (Psacharopoulos and Tzannatos 1989). Female participation is expected to peak before the onset of child-bearing and a few years after child-bearing, and decline during child-rearing (Mon 2000). Reddy (1979) notes that although, clearly, urban female activity rates are negatively associated with child-bearing and child-rearing age-groups, no such association is evident in rural areas. A possible explanation for this could be the predominance of the joint family system in rural areas, in which older women of the family take up the responsibility of child-rearing with older siblings also helping in the process (Reddy 1979). In Model I, AGE has a significant positive impact on female workforce participation whereas AGE_SQU has a negative significant effect, which shows the non-linear effect of age. Increase in age is associated with increased work participation up to a certain age, beyond which work participation decreases. This implies that younger women – who perform a greater share of household duties, as well as child-bearing and child-rearing activities – and older women are less likely to be in the workforce, as compared to middle-aged women. When we consider women’s paid employment (Model II), however, the age of the respondent is not significant in explaining female work participation in the study areas.
Although theoretically a positive correlation has been postulated between levels of education and female labour force participation, empirical findings from developing countries present mixed results (Standing 1981, cited in Ackah et al. 2009). In some cases, education and female participation rates show only a marginal or non-linear relationship (Mon 2000). According to a study by Psacharopoulos and Tzannatos (1989), education has an ambiguous effect on women’s participation in the labour force. Labour force participation rates are affected by the decision to participate in the labour market and the amount of time spent in the labour market.
Empirical studies also show that female labour participation is more responsive to wage (substitution effect) than to income; hence, the participation of educated women in the workforce is greater than the participation of women with little education (Psacharopoulos and Tzannatos 1989). In rural areas, non-farm paid jobs available to those with little education are equivalent to casual wage labour, where there is little association between wage levels and years of education. Education raises the reservation wage for these women by raising the productivity of time spent on their own farm and home production, which results in lower participation in wage/paid employment if the local labour market does not provide better opportunities (Unni 1994). This implies that women with some education may prefer to remain outside the labour market altogether, preferably doing household work or working on family farms as unpaid family labour in the absence of remunerative non-farm employment opportunities. A negative association between the level of education and female labour force participation in paid activities may thus be postulated in rural areas.
In the present analysis, the coefficient of education as measured by the number of years of schooling is negative but does not significantly affect female work participation rates in Model I. Since work participation in Model I includes both paid and unpaid activities, it is plausible that the level of education may weakly determine women’s participation in the workforce. In Model II, however, it is positive and statistically significant. The value of Exp (B) for EDUCATION in Model II is 1.129; that is, with a one-year increase in the number of years of schooling, the participation of women in paid employment increases by a factor of 1.129, or 12.9 per cent. An implication of this finding is that though the level of education has a non-significant effect on the work participation decisions, both paid and unpaid, of women, the level of education of women who are in paid employment is higher than those who are not. This also implies that women with a higher level of education are employed in non-farm jobs, as employment in agriculture is primarily as unpaid family labour.
In joint families with a large number of family members, a dichotomy is visible between men’s work and women’s work, with males being involved in paid activities and females in domestic activities. On the other hand, women of working age in joint families are helped in their domestic activities and child care by older women and other female members of the household (Reddy 1979), which in turn increases their participation in paid activities or agricultural activities on the family farm. In the study area, family structure (FAM_STR) is a dummy variable with the variable taking a value of 1 if the respondent belongs to a joint family and 0 otherwise. The coefficient for this dummy is negative and statistically significant for both models, indicating that a respondent who belongs to a joint family as compared to a nuclear family was less likely to be in the workforce. In Model I, the odds of participating in work for a respondent from a joint family decreased by a factor of 0.498 or 50.2 per cent, whereas in Model II, the odds decreased by a factor of 0.392 or 60.8 per cent. If there is a single earning member in a nuclear family, generally the husband, the wife is likely to work alongside him to supplement family labour on the farm or supplement family income through participation in paid activities. This explains the higher participation in the workforce of women belonging to nuclear families.
The presence of children may have a negative effect on women’s participation in economic activities (Chaykowski and Powell 1999). Younger children especially, i.e. children below the age of six, may cause women to spend more time in child care while the presence of older children may reduce their work burden. Cohen (1970) found that the presence of a child under the age of six was the most significant factor that determined labour force participation of married women (Anderson and Dimon 1998). In rural areas the presence of young children may not pose that much of a problem for women’s participation in agricultural activities, as older female children and female members of the household help with domestic work and childcare while older male children assist in some agricultural activities. However, the spread of primary and secondary education has meant that school-going children cannot help in childcare as before.
As mentioned above, in nuclear families the presence of small children, particularly below the age of six, may hinder a woman’s participation in economic activities. In the present study, the presence of children below the age of six was represented by the dummy variable CHILD_06, with the presence of one or more children below the age of six in the household being denoted by 1 and their absence by 0. In Model I, the presence of children under six years has a negative effect on female participation rates, but the results are not statistically significant. In Model II, however, the variable has a significant negative effect. The results indicate that for women with children less than six years of age, the odds of participating in paid work decreased by a factor of 0.115, or 88.5 per cent. Since paid work involves working away from the vicinity of the household as opposed to unpaid work on family farms, taking care of young children may hinder women’s participation in paid work.
The marital status of the respondent was another major influence on female labour force participation, as married women had greater household responsibilities than unmarried women (Mon 2000), which restricted their participation in the labour force. Being married influenced women’s decision-making ability, but increased the value of non-market activities. Women were expected to become mothers and homemakers, while men were viewed as breadwinners and heads of the household within patriarchal family structures (Blau et al. 1998, p. 13; Lisaniler and Bhatti 2005). Since such patriarchal family structures are widely prevalent in Indian society, marriage is expected to reduce the participation of women in labour market activities. We grouped the respondents into two categories: those currently married and those who were single/widowed/divorced/separated. The variable of marital status (MARITAL_STATUS) is a dummy with single/widowed/divorced/separated being the reference category. The results of the analysis show that for Model I, although the coefficient is positive, it is non-significant. For Model II, the coefficient is negative, implying that women in the single/widowed/divorced/separated category participated more in paid employment, but this is insignificant.
The decision of women to participate in the workforce is also influenced by the work status of their husbands. Women whose husbands have no source of income are more likely to work for cash, while those whose husbands are self-employed are more likely to work as unpaid family workers in the family business (Donahoe 1999). Nam (1991) found that in households where the male head was self-employed in the tertiary sector, or was employed as a family worker, or was unemployed, married women were two to three times more likely to participate in the labour market than those in families with a higher social status, controlling for age, number of children under the age of six, and marital status. Women whose household heads were blue-collar wage workers did not show high female labour force participation (Nam 1991). In our analysis, the primary occupation of the head of the household, whether agricultural or non-agricultural, was considered a determinant of female work participation. The dummy variable (OCCUPATION_HEAD) took a value of 1 if the primary occupation was agriculture and 0 if it was non-agriculture. For Model I, the occupation of the head of the household is significant in explaining the work participation of the respondents, with the odds of a respondent participating in the workforce increasing by a factor of 2.566 if the occupation of the household head is agriculture. This implies that the odds of being in the workforce for women in agricultural households increases by almost three times, as against women in non-agricultural households. These results highlight the significant role played by women in agricultural activities. For Model II, the variable OCCUPATION_HEAD, although negative, does not have a significant effect on women’s work participation.
Male migration has been significant in rural areas, particularly in the hill and mountain areas, from where men have moved to lowland areas in search of better employment opportunities. This increases the drudgery and work burden of women in these regions as they have to take on tasks previously performed by men (Pande 1996). A study of labour out-migration of rice-farming households in three districts of eastern Uttar Pradesh also reports an increase in the workload of women in nuclear households in the absence of males. The study shows that women took over many male-specific activities in rice farming (Paris et al. 2005).
The impact of male migration on the labour market behaviour of women, however, is ambiguous. A theoretical model developed by Lokshin and Glinskaya (2009) predicts that male migration could have two effects on female labour market participation. First, the increase in household income from remittances could lead to a reduction in labour market participation of women. Secondly, depending on the properties of the home production function, male migration could increase or decrease women’s productivity at home, thus rendering their effect on labour market participation ambiguous. The overall effect of male migration on women’s labour market participation therefore depends on the interaction of these factors.
To understand the effect of male migration on female work participation, the presence of a male migrant (MIGRANT) has been included in the present model as a dummy variable, with respondents in households with at least one male migrant being coded as 1 and households with no male migrants as 0. Though the presence of male migrants affects female work participation inversely in both models, it is not significant. The non-significant effect of MIGRANT in Model I is plausible, where both paid and unpaid activities of females have been considered. Irrespective of the presence of a male migrant, women in rural households participate in paid as well as unpaid activities. In Model II, women in households with at least one male migrant are less likely to participate in paid activities as household income may increase as a result of remittances (Lokshin and Glinskaya 2009). Women may also be forced to stay at home to perform household chores that were earlier performed by men, thus increasing their participation in unpaid domestic activities and leaving less time for participation in paid activities. This is contrary to the belief that male migration increases the participation of women in the workforce. The hypothesis that male out-migration increases the work participation of women can thus be rejected in the present study.
Family income has been noted as an important determinant of female work participation. Nayyar (1987) writes, “several scholars have pointed out that poverty is the single most important factor influencing female participation rates, which cuts across regions, religions, age, and time.” Low levels of earnings among males induce females to participate in economic activities to supplement family income, a phenomenon referred to as the “additional worker effect” (Reddy 1979). Alternatively, the participation of women in the labour market leads to an increase in total family income, thereby postulating a positive relation between female labour force participation and total household income.
To avoid endogeneity in the present study, household income was approximated by using monthly per capita consumption expenditure (MPCE) as a proxy for family income. Estimated household expenditure is a better indicator of living standards than estimated income, particularly in household surveys in developing countries (Mailu et al. n. d.). The univariate analysis for household MPCE was statistically insignificant in both models. This implies that women in rural areas, irrespective of the level of expenditure or income, participate in economic activities, both paid and unpaid.
Land is not only a vital asset in agricultural families, but also an indicator of socio-economic status. Some micro studies have established a negative correlation between landlessness and female participation rates in rural areas in India. Given that landlessness is an indicator of poverty in rural areas, it appears logical that women in the landless category participate more in economic activities to supplement family income than women with land (Nayyar 1987). Some studies, however, find a positive relationship between women’s work participation and the size of landholding (Bhati and Singh 1987). In our study, we have measured the landholdings of households in acres. The results, according to the univariate analysis, indicate a non-significant relation between the size of landholding and female work participation (and were thus not included in the logistic regression exercise). Since the study considers paid as well as unpaid work, land does not appear statistically significant as women in families with small or large holdings may be employed as unpaid labour on the family farm. Low prevalence of agricultural labour, and fewer stringent class and caste distinctions in the hill areas (relative to the plains) may also help explain the non-significant effect of land on women’s paid and unpaid labour on family farms. In Model II, however, the size of land owned by the family is statistically significant in explaining women’s work participation in paid activities. The odds of a respondent participating in paid employment decreased by a factor of 0.47 or 53 per cent for every one-acre increase in land owned by the household. This can be attributed to the fact that smaller landholdings mean lower income from agriculture, inducing women to search for paid employment outside the household, in agriculture or non-agriculture.
Conclusions
Our analysis shows that women’s employment in the rural hill regions of West Bengal is characterised by a predominance of unpaid work as family labour in agriculture. While 71.9 per cent of working-age women in the study were employed in paid as well as unpaid employment, only 14.5 per cent reported active participation in paid employment. This highlights the crucial role that women in the rural hill economy play through their involvement in unpaid farm employment and allied work.
The findings of the study show that the age of women has a non-linear effect on their participation in economic activities (paid as well as unpaid work). However, age does not show a significant effect on women’s work decisions, if we consider only paid work. This implies that younger women – on account of child-bearing and child-rearing activities, and other household work – and older women may not participate in economic activities as much as women in the middle of the age distribution.
The results of the study also indicate the significant positive effect of education on women’s involvement in paid work. Women with higher levels of education preferred to take up jobs outside the agricultural sector, either in self-employment or wage employment. Self-employment in the region included petty trade, such as running a shop in the vicinity of the household, while wage employment included teaching, working as an ICDS helper, a mid-day meal cook or in a government office. Wage employment in agriculture was not common due to the prevalence of the labour exchange system of “parma.”
The structure of the family was also an important determinant of women’s labour market behaviour, with women in nuclear families participating more in the labour market than women in joint families. The presence of a single male breadwinner and the desire to augment family income in order to improve living standards contribute to higher work participation among women in nuclear families. This suggests a higher work burden for women in nuclear families where there is very little sharing of domestic responsibilities. The study also shows that the presence of children under the age of six in the household lowered women’s participation in paid work. The marital status of women was insignificant in determining women’s involvement in economic activities in both models, although women’s marital status and women’s work participation had an inverse relation in the two models.
The presence of a male migrant in the family and the per capita consumption level of the household, a proxy for household income, had no significant effect on the work participation of women in the study. This is in contrast to studies that report higher female participation because of male out-migration. Finally, size of landholding was found to influence women’s participation in paid activities in the study area, with women in households with smaller landholdings showing a higher likelihood of participating in paid activities.
Since women in the rural hill region make significant contributions to family farms as unpaid labour, it is important to recognise their contributions through a proper valuation of their services. Recognising women as farmers, and increasing their skills through training and education, along with provision of extension services, would help improve the position of women involved in farm activities. Diversification towards non-traditional agricultural activities such as horticulture, apiculture, and pisciculture would also help augment family income and improve rural well-being. Further, new jobs in the non-farm sector can increase the participation of women in paid work. Opportunities for self-employment in various farm and non-farm activities can also be explored, such as processing dairy products, pickling, production of jams and juices, handicrafts, and eco-tourism. The limiting effect of fertility on women’s paid employment can be offset through the provision of child-care facilities at work.
Notes
1 At present (that is, since March 30, 2017) Darjeeling district has four sub-divisions: Darjeeling Sadar, Kurseong, Mirik – which was carved out of Kurseong sub-division on March 30, 2017 – and Siliguri. Kalimpong became a separate district on February 14, 2017.
2 “Parma” is a system of direct labour exchange between two households in which the members of the households work on each other’s land on alternate days (Subba 1985, p. 35).
3 This is not a matter for concern as the p-value of the squared term is not affected by multicollinearity. High correlation can be reduced by centering the variables (i.e. by subtracting the means) before squaring, which will have no effect on the p-value of the squared term or results for other variables including R-squared, but not the lower order terms. This means that multicollinearity is not a problem (Allison 2012).
4 The R2 of a linear regression model and the pseudo R2 of a choice model show a direct empirical relationship (Domencich and McFadden 1975), with pseudo R2 values between the range 0.3 and 0.4 being translated as an R2 between 0.6 and 0.8 for the linear model equivalent (Hensher et al. 2005, pp. 338–9).
5 The pseudo R2 as shown by Nagelkerke R-square is 0.476 and 0.318 for Model I and Model II, respectively, and the model fit is quite satisfactory for both models.
References
| Ackah, Charles, Ahiadeke, Clement, and Fenny, Ama Pokuaa (2009), “Determinants of Female Labour Force Participation in Ghana,” Working Paper Number 14, GDN Working Paper Series, Global Development Network, Washington D. C. | |
| ActionAid (2017), Invisible Work, Invisible Workers: The Sub-Economies of Unpaid Work and Paid Work, Action Research on Women’s Unpaid Labour, ActionAid Association, New Delhi. | |
| Afifi, Abdelmonem, May, Susanne, and Clark, Virginia A. (2012), Practical Multivariate Analysis, fifth edition, CRC Press, Boca Raton. | |
| Agarwal, Bina (1997), “‘Bargaining’ and Gender Relations: Within and Beyond the Household,” Feminist Economics, vol. 3, no. 1, pp. 1–51. | |
| Allison, Paul (2012), “When You can Safely Ignore Multicollinearity,” available at https://statisticalhorizon.com/blog, viewed on June 1, 2018. | |
| Anderson, Joan B., and Dimon, Denise (1998), “Married Women’s Labour Force Participation in Developing Countries: The Case of Mexico,” Estudios Económicos, vol. 13, no. 1(25), January–June, pp. 3–34. | |
| Bhati, J. P., and Singh, D.V. (1987), “Women’s Contribution to Agricultural Economy in Hill Regions of North-West India,” Economic and Political Weekly, vol. 22, no. 17, April 25, pp. WS-7-WS-11. | |
| Blau, F. D., Ferber, M. A., and Winkler, A. E. (1998), The Economics of Women, Men, and Work (Third edition), Prentice Hall, London. | |
| Chakraborty, I., and Chakraborty, A. (2009), “Female Work Participation and Gender Differential in Earning in West Bengal,” Occasional Paper Number 18, Institute of Development Studies Kolkata, Kolkata. | |
| Chaykowski, Richard P., and Powell, Lisa M. (1999), “Women and the Labour Market: Recent Trends and Policy Issues,” Canadian Public Policy/Analyse de Politiques (Supplement: Women in the Canadian Labour Market), vol. 25, November, pp. S1–S25. | |
| Cohen, Malcolm S. (1970), A Micro Model of Labour Supply, Government Printing Office, Washington D. C. | |
| Domencich, T., and McFadden, D. (1975), Urban Travel Demand: A Behavioural Analysis, Elsevier, New York and Oxford. | |
| Donahoe, Debra Anne (1999), “Measuring Women’s Work in Developing Countries,” Population and Development Review, vol. 25, no. 3, September, pp. 543–76. | |
| England, Paula, and Kilbourne, Barbara (1990), “Markets, Marriages, and other Mates: The Problem of Power,” in R. Friedman and A. F. Robertson (eds.), Beyond the Market: Rethinking Economy and Society, Aldine de Gruyter, New York. | |
| Government of India (GoI) (2013), Key Indicators of Employment and Unemployment in India, 2011–2012, NSS 68th Round, National Sample Survey Office, Ministry of Statistics and Programme Implementation, Government of India, New Delhi. | |
| Government of India (GoI) (2014), Household Consumption of Various Goods and Services in India 2011–12, NSS 68th Round, National Sample Survey Office (NSSO), Ministry of Statistics and Programme Implementation, Government of India, New Delhi. | |
| Gujarati, Damodar N. (2004), Basic Econometrics, fourth edition, McGraw-Hill, New York. | |
| Hensher, David A., Rose, John M., and Green, William H. (2005), Applied Choice Analysis: A Primer, Cambridge University Press, Cambridge. | |
| Hosmer, David W., and Lemeshow, Stanley (2002), Applied Logistic Regression, second edition, John Wiley and Sons, New York. | |
| International Labour Organisation (ILO) (2012), Global Employment Trends for Women, International Labour Organisation, Geneva. | |
| Lisaniler, Fatma Güven, and Bhatti, Feyza (2005), “Determinants of Female Labour Force Participation: A Study of North Cyprus,” Review of Social, Economic, and Business Studies, vol. 5/6, pp. 209–26. | |
| Lokshin, Michael, and Glinskaya, Elena (2009), “The Effect of Male Migration on Employment Patterns of Women in Nepal,” The World Bank Economic Review, vol. 23, no. 3, pp. 481–507. | |
| Mailu, S. K., Maritim, H. K., Yabann, W. K., and Muhammed, L. (n. d.), “Household Income Versus Household Expenditure: An Illustration of the Superiority of Household Expenditure as an Estimator of Living Standards,” Kenya Agricultural Research Institute, available at http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=A83811037466379117899971BEBF2B81?doi=10.1.1.197.791&rep=rep1&type=pdf, viewed on July 20, 2018. | |
| Mon, Myat (2000), “Determinants of Female Labour Force Participation in Burma: An Empirical Analysis of Socio-Economic Survey Data,” ABAC Journal, vol. 21, no. 1, January–April. | |
| Nam, Sunghee (1991), “Determinants of Female Labour Force Participation: A Study of Seoul, South Korea, 1970–1980,” Sociological Forum, vol. 6, no. 4, December, pp. 641–59. | |
| Nayyar, Rohini (1987), “Female Participation Rates in Rural India,” Economic and Political Weekly, vol. 22, no. 51, December 19, pp. 2207–09, 2211–16. | |
| Pande, P. N. (1996), Drudgery of the Hill Women, Indus Publishing Company, New Delhi. | |
| Paris, Thelma, Singh, Abha, Luis, Joyce, and Hossain, Mahabub (2005), “Labour Outmigration, Livelihood of Rice Farming Households, and Women Left Behind: A Case Study in Eastern Uttar Pradesh,” Economic and Political Weekly, vol. 40, no. 25, June 18–24, pp. 2522–29. | |
| Psacharopoulos, George, and Tzannatos, Zafiris (1989), “Female Labour Force Participation: An International Perspective,” The World Bank Research Observer, vol. 4, no. 2, July, pp. 187–201. | |
| Reddy, D. Narasimha (1979), “Female Work Participation in India: Facts, Problems, and Policies,” Indian Journal of Industrial Relations, vol. 15, no. 2, October, pp. 197–212. | |
| Sen, Amartya K. (1990), “Gender and Co-operative Conflicts,” in Irene Tinker (ed.), Persistent Inqualities: Women and World Development, Oxford University Press, New York, pp. 123–49. | |
| Srivastava, Nisha, and Srivastava, Ravi (2010), “Women, Work, and Employment Outcomes in Rural India,” Economic and Political Weekly, vol. 45, no. 28, July 10, pp. 49–63. | |
| Standing, Guy (1981), Labour Force Participation and Development, International Labour Office, Geneva. | |
| Subba, T. B. (1985), The Quiet Hills: A Study of Agrarian Relations in Hill Darjeeling, Cambridge University Press, New Delhi. | |
| Sundar, P. (1981) “Characteristics of Female Employment: Implications of Research and Policy,” Economic and Political Weekly, vol. 16, no. 19, May 9, pp. 863–71. | |
| United Nations Development Programme (UNDP) (1995), Human Development Report 1995, United Nations Development Programme, Oxford University Press, New York. | |
| Unni, Jeemol (1994), “Labour Participation Decisions of Married Women in Rural India,” Indian Economic Review, New Series, vol. 29, no. 2, July–December, pp. 177–93. |
Appendix
Model Specification
Given the dichotomous nature of the response variable, binary logistic regression has been used in the present analysis. The dependent variable (Y) is female work participation, which can take only two values: Yi = 1 if the respondent is in the workforce, and Yi = 0 if the respondent is not in the workforce. The predictor variables Xis, also known as covariates, may be numerical or categorical in nature. For a categorical variable, a dummy variable is used. If Pi represents the probability of the ith female respondent being in the workforce, the model may be written as:
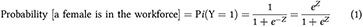
where Z is a linear function of the explanatory variables. If X1, X2, ...,Xk represent the various explanatory variables, then “Z” equation would be:
Zi = βo + β1 X1 + β2 X2 + ... + β k X k
Xi = ith Explanatory variables (i = 1, 2, ..., k) and
βi = parameters of the model (i = 0, 1, 2, ..., k)
In the above equation Pi is non-linear not only in Xis, but also in βs. It can be linearised in the following manner:
Probability [a female is not in the workforce] = 1–Pi(Y = 1)
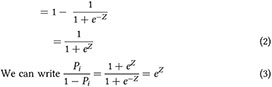
Here 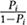 are the odds in favour of a female participating in the workforce, which is the ratio of the probability of an event occurring to the probability of the event not occurring. Taking the natural logarithm of the odds, we get
are the odds in favour of a female participating in the workforce, which is the ratio of the probability of an event occurring to the probability of the event not occurring. Taking the natural logarithm of the odds, we get
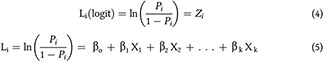
Now, Li, the log of the odds, is linear not only in Xis but also in the βs, and is termed the logit (Gujarati 2004, pp. 595–96). As the value of Pi varies from 0 to 1, the odds vary from 0 to ∞. When Pi = 0.5, the odds are 1. On the odds scale, the values from 0 to 1 correspond to values of Pi from 0 to 0.5. On the other hand, values of Pi from 0.5 to 1 result in odds of 1 to ∞. Taking the natural logarithm of the odds cures this asymmetry. When Pi = 0, ln (odds) = −∞; when Pi = 0.5, ln (odds) = 0.0; and when Pi = 1, ln (odds) =+∞ (Afifi et al. 2012, p. 272). This implies that although the probabilities lie between 0 and 1, the logit is not bounded and can lie between –∞ and +∞, and as such can have an unlimited range of values. The link function (the function of the dependent variable that yields a linear function of the independent variables) in the logistic regression model is therefore the logit transformation (Hosmer and Lemeshow 2002, p. 48).
For easier interpretation, the log odds can be converted into an odds ratio, or the ratio of the odds of occurrence of an event between two situations. If we consider two values of the categorical independent variable X, where X=0 and X=1, the odds ratio for Y=1 may be written as:
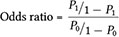
where P1 is the probability of Y=1 for X=1, and P0 is the probability of occurrence of Y=1 for X=0. The numerator therefore represents the odds in favour of the event Y for X=1, and the denominator represents the odds in favour of Y for X=0 (ibid., pp. 48–50).
Multicollinearity in the Model
The rule of thumb is that if the pair-wise or zero-order correlation coefficient between two regressors is high, for example, in excess of 0.8, multicollinearity is a serious problem (Gujarati 2004, p. 359). Eigen values and condition indices may also be used on occasion to detect the presence of multicollinearity.
Appendix Table 1 Correlation matrix of explanatory variables
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | |
| X1 | 1 | |||||||||
| X2 | 0.068 | 1 | ||||||||
| X3 | 0.177 | 0.051 | 1 | |||||||
| X4 | −0.010 | −0.068 | 0.108 | 1 | ||||||
| X5 | 0.074 | −0.054 | −0.078 | −0.034 | 1 | |||||
| X6 | −0.065 | 0.076 | 0.113 | 0.033 | −0.145 | 1 | ||||
| X7 | 0.173 | 0.024 | 0.008 | −0.025 | −0.070 | −0.062 | 1 | |||
| X8 | −0.430 | 0.028 | −0.344 | 0.176 | 0.047 | −0.031 | 0.053 | 1 | ||
| X9 | −0.213 | 0.210 | −0.029 | −0.179 | −0.143 | 0.113 | 0.038 | 0.283 | 1 | |
| X10 | 0.136 | 0.167 | −0.130 | −0.046 | 0.266 | 0.011 | 0.138 | −0.013 | −0.024 | 1 |
Note: X1–EDUCATION, X2–FAM_STR, X3–CHILD_06, X4–MARITAL_STATUS, X5–OCCUPATION_HEAD, X6–MIGRANT, X7–MPCE, X8–AGE, X9–AGE_SQU, X10– LAND
In the present analysis, the pair-wise correlation coefficients between the regressors exhibit values less than the cut-off value of 0.8 (Appendix Table 1). Further, for both models, the values of tolerance, VIF, Eigen value, and condition indices are well within the cut-off range to rule out multicollinearity among the predictors (Appendix Tables 2 and 3).
Appendix Table 2 Tolerance, variance inflation factor (VIF), and collinearity diagnostics for Model I
| Variables | Tolerance | VIF | Dimension | Eigen value | Condition index |
| EDUCATION | 0.780 | 1.282 | 1 | 4.606 | 1.000 |
| FAMILY_STR | 0.935 | 1.070 | 2 | 1.366 | 1.836 |
| CHILD_06 | 0.828 | 1.207 | 3 | 0.848 | 2.330 |
| MARITAL_STATUS | 0.862 | 1.161 | 4 | 0.624 | 2.718 |
| OCCUPATION_HEAD | 0.941 | 1.062 | 5 | 0.553 | 2.887 |
| MIGRANT | 0.949 | 1.054 | 6 | 0.384 | 3.462 |
| AGE | 0.629 | 1.589 | 7 | 0.335 | 3.708 |
| AGE_SQU | 0.784 | 1.275 | 8 | 0.215 | 4.632 |
| Mean of VIFs | 1.213 | 9 | 0.069 | 8.169 | |
Appendix Table 3 Tolerance, variance inflation factor (VIF), and collinearity diagnostics for Model II
| Variables | Tolerance | VIF | Dimension | Eigen value | Condition index |
| EDUCATION | 0.769 | 1.300 | 1 | 5.215 | 1.000 |
| FAMILY_STR | 0.904 | 1.106 | 2 | 1.372 | 1.950 |
| CHILD_06 | 0.809 | 1.236 | 3 | 0.894 | 2.416 |
| MARITAL_STATUS | 0.862 | 1.161 | 4 | 0.652 | 2.829 |
| OCCUPATION_HEAD | 0.875 | 1.143 | 5 | 0.557 | 3.061 |
| MIGRANT | 0.945 | 1.058 | 6 | 0.385 | 3.678 |
| AGE | 0.629 | 1.590 | 7 | 0.356 | 3.828 |
| AGE_SQU | 0.784 | 1.275 | 8 | 0.287 | 4.262 |
| LAND | 0.861 | 1.161 | 9 | 0.215 | 4.929 |
| Mean of VIFs | 1.226 | 10 | 0.068 | 8.737 | |
Selection of Variables
Prior to inclusion of a variable in the logistic model, we carried out a univariate analysis of each variable (Appendix Tables 4 and 5). Any variable whose univariable test has a p-value < 0.25 is a candidate for the multivariable model (Hosmer and Lemeshow 2002).
Appendix Table 4 Univariate analysis for Model I (dependent variable – FLFP)
| FLFP | B | S. E. | Wald | df | Sig. | Exp(B) | |
| Step 1a | AGE | 0.106 | 0.018 | 33.071 | 1.000 | 0.000 | 1.112 |
| Step 1a | AGE_SQU | −0.004 | 0.001 | 16.703 | 1.000 | 0.000 | 0.996 |
| Step 1a | EDUCATION | −0.080 | 0.032 | 6.183 | 1.000 | 0.013 | 0.923 |
| Step 1a | FAM_STR (1) | −0.845 | 0.306 | 7.633 | 1.000 | 0.006 | 0.430 |
| Step 1a | CHILD_06 (1) | −1.221 | 0.369 | 10.959 | 1.000 | 0.001 | 0.295 |
| Step 1a | MARITAL_STATUS (1) | 1.062 | 0.321 | 10.964 | 1.000 | 0.001 | 2.894 |
| Step 1a | OCCUPATION_HEAD (1) | 0.965 | 0.299 | 10.411 | 1.000 | 0.001 | 2.624 |
| Step 1a | MIGRANT (1) | −0.660 | 0.334 | 3.920 | 1.000 | 0.048 | 0.517 |
| Step 1a | MPCE | 0.034 | 0.081 | 0.175 | 1.000 | 0.676 | 1.034 |
| Step 1a | LAND | −0.025 | 0.080 | 0.099 | 1.000 | 0.754 | 0.975 |
Note: a. Variable(s) entered for step 1: AGE / AGE_SQU / EDUCATION / FAM_STR / CHILD_06 / MARITAL_STATUS / OCCUPATION_HEAD / MIGRANT / MPCE / LAND.
Thus, MPCE and LAND have been excluded as explanatory variables for Model I. For Model II, AGE and MPCE have p values < 0.25. However, as AGE_SQU is statistically significant, both AGE and AGE_SQU have been included as explanatory variables but MPCE has been excluded.
Appendix Table 5 Univariate analysis for Model II (dependent variable – FLFP_PAID)
| FLFP_PAID | B | S. E. | Wald | df | Sig. | Exp(B) | |
| Step 1a | AGE | −0.008 | 0.017 | 0.238 | 1.000 | 0.625 | 0.992 |
| Step 1a | AGE_SQU | −0.004 | 0.002 | 4.196 | 1.000 | 0.041 | 0.996 |
| Step 1a | EDUCATION | 0.084 | 0.038 | 5.056 | 1.000 | 0.025 | 1.088 |
| Step 1a | FAM_STR(1) | −1.186 | 0.403 | 8.686 | 1.000 | 0.003 | 0.305 |
| Step 1a | CHILD_06(1) | −1.974 | 1.032 | 3.662 | 1.000 | 0.056 | 0.139 |
| Step 1a | MARITAL_STATUS (1) | −0.477 | 0.403 | 1.401 | 1.000 | 0.237 | 0.621 |
| Step 1a | OCCUPATION_HEAD (1) | −0.507 | 0.374 | 1.839 | 1.000 | 0.175 | 0.602 |
| Step 1a | MIGRANT(1) | −1.176 | 0.627 | 3.520 | 1.000 | 0.061 | 0.308 |
| Step 1a | MPCE | 0.014 | 0.100 | 0.020 | 1.000 | 0.888 | 1.014 |
| Step 1a | LAND | −0.649 | 0.246 | 6.962 | 1.000 | 0.008 | 0.523 |
Note: a. Variable(s) entered on step 1: AGE / EDUCATION / FAM_STR / CHILD_06 / MARITAL_STATUS / OCCUPATION_HEAD / MIGRANT / MPCE / LAND
Summary Statistics
Appendix Table 6 shows the mean and standard deviation of the explanatory variables used in the two models. The average age of women in the labour force in Model I (40.9) is higher than that in Model II (37.2). The level of education as measured by years of schooling for women who are in the workforce is higher for Model II (8.7) than for Model I (6.11). The average size of landholding of women in the workforce in Model II is lower than that in Model I, whereas the average monthly per capita consumption expenditure of women who are in the workforce is almost equal in the two models. The average monthly per capita consumption expenditure for women who are in the workforce for Model I is Rs 2,867.81 and Rs 2,877.35 for Model II; and the average size of landholding is 1.97 acres for Model I and 1.26 acres for Model II. For the categorical explanatory variables, for example, a mean of 0.48 for FAMILY_STR for FLFP = 1 implies that 48 per cent of women in the workforce in Model I are in joint families.
Appendix Table 6 Summary statistics of the explanatory variables
| Explanatory variables | Model I | Model II | ||||||
| FLFP = 1 N = 169 | FLFP = 0 N = 66 | FLFP_PAID = 1 N = 34 | FLFP_PAID = 0 N = 201 | |||||
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | |
| AGE | 40.97 | 9.38 | 30.94 | 11.98 | 37.29 | 8.59 | 38.3 | 11.5 |
| EDUCATION | 6.11 | 5.19 | 8.08 | 4.39 | 8.71 | 7.91 | 6.32 | 4.31 |
| FAMILY_STR | 0.48 | 0.5 | 0.68 | 0.47 | 0.29 | 0.46 | 0.58 | 0.5 |
| CHILD_06 | 0.11 | 0.31 | 0.29 | 0.46 | 0.03 | 0.17 | 0.18 | 0.38 |
| MARITAL_STATUS | 0.82 | 0.39 | 0.61 | 0.49 | 0.68 | 0.48 | 0.77 | 0.42 |
| OCCUPATION_HEAD | 0.62 | 0.49 | 0.38 | 0.49 | 0.44 | 0.5 | 0.57 | 0.5 |
| MIGRANT | 0.18 | 0.39 | 0.3 | 0.46 | 0.09 | 0.29 | 0.24 | 0.43 |
| MPCE | 2.87 | 1.72 | 2.76 | 2.11 | 2.88 | 1.56 | 2.83 | 1.88 |
| LAND | 1.97 | 1.73 | 9.34 | 1.92 | 1.26 | 0.87 | 2.12 | 1.87 |
| Sample size | 235 | 235 | ||||||
Evaluation of the Logistic Regression Model
Likelihood Ratio Test
The likelihood ratio (LR) statistic, or Omnibus Test of Model Coefficients, using SPSS version 23, is shown in Appendix Table 7. For both models, the chi-square was significant, indicating that at least one of the predictors is significantly related to the outcome variable. Since all variables have been entered at the same time, there is no difference between step, block or model chi-square values.
Appendix Table 7 Omnibus tests of model coefficients – Model I and Model II
| Model I Dependent variable = FLFP | Model II Dependent variable = FLFP_PAID | ||||||||
| Chi-square | df | Sig. | Chi-square | df | Sig. | ||||
| Step 1 | Step | 94.443* | 8 | 0.000 | Step 1 | Step | 46.268# | 9 | 0.000 |
| Block | 94.443 | 8 | 0.000 | Block | 46.268 | 9 | 0.000 | ||
| Model | 94.443 | 8 | 0.000 | Model | 46.268 | 9 | 0.000 | ||
Notes: * Initial –2 Log Likelihood = 279.065, Model –2 Log Likelihood = 184.622, hence LR statistic = 279.065–184.622=94.443
# Initial –2 Log Likelihood = 194.284, Model –2 Log Likelihood = 148.016, hence LR statistic = 194.284–148.016= 46.268.
Hosmer and Lemeshow Goodness of Fit
The Hosmer–Lemeshow (H–L) statistic (Appendix Table 8) for both models yields a desirable outcome of non-significance (p = 0.636 for Model I and p = 0.557 for Model II), indicating that the predicted model does not significantly differ from the observed model.
Appendix Table 8 Hosmer and Lemeshow goodness of fit test
| Model I Dependent Variable – FLFP | Model II Dependent Variable – FLFP_PAID | ||||||
| Step | Chi-square | df | Sig. | Step | Chi-square | df | Sig. |
| 1 | 6.101 | 8 | 0.636 | 1 | 6.812 | 8 | 0.557 |
R2 Equivalents for Logistic Regression/Pseudo R-square
In SPSS, the two most commonly used measures of Pseudo R-square are Cox and Snell R-square and Nagelkerke R-square. Another measure, reported by EViews, is the McFadden R-square. Values of the Pseudo R-square for both models are shown in Appendix Table 9.4, 5
Appendix Table 9 Values of pseudo R2
| Model I (Dependent variable – FLFP) | Model II (Dependent variable – FLFP_PAID) | |
| McFadden R-square | 0.338 | 0.238 |
| Cox and Snell R-square | 0.331 | 0.179 |
| Nagelkerke R-square | 0.476 | 0.318 |
Notes: (i) Estimation terminated at iteration number 5 because parameter estimates changed by less than 0.001.
(ii) Estimation terminated at iteration number 6 because parameter estimates changed by less than 0.001.
Classification Table
The classification table for Model I (Appendix Table 10) shows that the model correctly predicts 81.3 per cent of observations as compared to the constant only model. Sensitivity, defined as the proportion of observations with Y = 1 that are correctly predicted by the model, is 91.7 per cent, and specificity, defined as the proportion of observations with Y = 0 that are correctly predicted by the model, is 54.5 per cent. The estimated equation is 9.4 per cent better at predicting responses than the constant only model.
Appendix Table 10 Classification table – Model I
| Observed | Predicted | Observed | Predicted | ||||||
| FLFP | Percentage correct | FLFP | Percentage correct | ||||||
| 0 | 1 | 0 | 1 | ||||||
| Step 0 a b | FLFP | 0 | 0 | 66 | 0 | Step 1b | 36 | 30 | 54.5 |
| 1 | 0 | 169 | 100 | 14 | 155 | 91.7 | |||
| Overall Percentage | 71.9 | 81.3 | |||||||
Notes: (i) Constant is included in the model.
(ii) The cut-off value is 0.500.
The classification table for Model II (Appendix Table 11) shows that the model correctly predicts 88.1 per cent of observations as compared to the constant only model. Sensitivity is 20.6 and specificity is 99.5 per cent. The estimated equation is 2.6 per cent better at predicting responses than the constant only model.
Appendix Table 11 Classification table for Model II
| Observed | Predicted | Observed | Predicted | ||||||
| FLFP_PAID | Percentage correct | FLFP_PAID | Percentage correct | ||||||
| 0 | 1 | 0 | 1 | ||||||
| Step 0 a b | FLFP_PAID | 0 | 201 | 0 | 100 | Step 1 | 200 | 1 | 99.5 |
| 1 | 34 | 0 | 0 | 27 | 7 | 20.6 | |||
| Overall Percentage | 85.5 | 88.1 | |||||||
Notes: (i) Constant is included in the model.
(ii) The cut-off value is 0.500.
The full model, including all predictor variables, was tested against the constant only model and found to be statistically significant (Chi-square = 94.443 for Model I at p = 0.000 at 8 degrees of freedom, and Chi-square = 46.268 for Model II at p = 0.000 at 9 degrees of freedom as shown in Appendix Table 7). The Pseudo R-square values (Cox and Snell R-square = 0.331, Nagelkerke R-square = 0.476, and McFadden R-square = 0.338) for Model I show that 33 to 48 per cent of the variations in female work participation are explained by the set of predictor variables. The Pseudo R-square values for Model II are Cox and Snell R-square = 0.179, Nagelkerke R-square = 0.318, and McFadden R-square = 0.238. The percentage of correct predictions by the model is 81.3 per cent for Model I and 88.1 per cent for Model II.


